题目内容
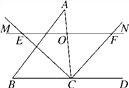
【题目】如图,![]() 是等边三角形,
是等边三角形,![]() 分别是边
分别是边![]() 上的点,且
上的点,且![]() ,且
,且![]() 交于点
交于点![]() ,且
,且![]() ,垂足为
,垂足为![]() .
.

(1)求证: ![]() ;
;
(2)若![]() ,求
,求![]() 的长度.
的长度.
【答案】(1)证明见解析;(2)2
【解析】
(1)证明△ACE≌△CBF(SAS),即可证得结论;
(2)利用由(1)知∠ACE=∠CBF,求出∠BPE=60°,又EG⊥BF,即∠PGE=90°,得到∠GEP=30°,根据在直角三角形中,30°所对的直角边等于斜边的一半即可求得答案.
∵△ABC为等边三角形,
∴AC =BC,∠A=∠BCF=60°,
在△ACE和△CBF中, ,
,
∴△ACE≌△CBF(SAS),
∴∠ACE=∠CBF;
(2)由(1)知∠ACE=∠CBF,
又∠ACE +∠BCE=∠ACB=60°,
∴∠CBF +∠BCE =60°,
∵∠CBF +∠BCE =∠BPE,
∴∠BPE=60°,
∵EG⊥BF,即∠PGE=90°,
∴∠GEP=30°,
∴在Rt△BCE中,
PE=2PG=2.


练习册系列答案
相关题目