题目内容
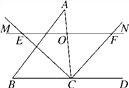
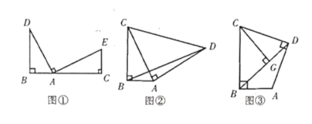
【题目】(l)观察猜想:如图①,点![]() 、
、![]() 、
、![]() 在同一条直线上,
在同一条直线上,![]() ,
,![]() 且
且![]() ,
,![]() ,则
,则![]() 和
和![]() 是否全等?__________(填是或否),线段
是否全等?__________(填是或否),线段![]() 之间的数量关系为__________
之间的数量关系为__________
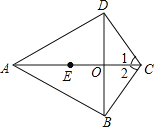
(2)问题解决:如图②,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以
,以![]() 为直角边向外作等腰
为直角边向外作等腰![]() ,连接
,连接![]() ,求
,求![]() 的长。
的长。
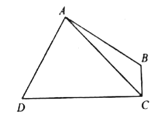
(3)拓展延伸:如图③,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 于点
于点![]() .求
.求![]() 的长.
的长.
【答案】(1)是,![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据垂直的定义,直角三角形的性质证得∠D=∠CAE,即可利用AAS证明△BAD≌△CEA,即可得到答案;
(2)过![]() 作
作![]() ,交
,交![]() 的延长线于
的延长线于![]() ,利用勾股定理求出BC,根据(1)得到
,利用勾股定理求出BC,根据(1)得到![]() ,再利用勾股定理求出BD;
,再利用勾股定理求出BD;
(3)过![]() 作
作![]() 于
于![]() ,作
,作![]() 于
于![]() ,连接
,连接![]() ,利用勾股定理求出BC,证明
,利用勾股定理求出BC,证明![]() 得到四边形BEFD是正方形,即可求出CG.
得到四边形BEFD是正方形,即可求出CG.
(1)∵![]() ,
,![]() ,
,
∴∠B=∠C=![]() ,
,
∴∠BAD+∠D=∠BAD+∠CAE=90![]() ,
,
∴∠D=∠CAE,
∵![]() ,
,
∴△BAD≌△CEA,
∴AB=CE,BD=AC,
故答案为:是,![]() ;
;
(2)问题解决
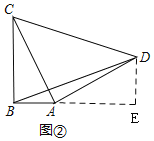
如图②,过![]() 作
作![]() ,交
,交![]() 的延长线于
的延长线于![]() ,
,
由(1)得:![]() ,
,
在![]() 中,由勾股定理得:
中,由勾股定理得:![]()
![]() ,
,
![]() 中,
中,![]() ,
,
由勾股定理得: ![]()
(3)拓展延伸
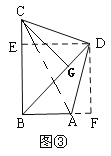
如图③,过![]() 作
作![]() 于
于![]() ,作
,作![]() 于
于![]() ,连接
,连接![]()
∵![]() ,
,![]() ,
,![]() ,
,
∴AC=13,
∵![]() ,
,
∴BC=12,
∵![]() ,
,![]() ,
,
∴∠DEB=∠DFB=90![]() ,
,
∴四边形BEFD是矩形,
∴∠EDF=90![]() ,
,
∴∠EDC=∠ADF,
∴![]() ,
,
∴ED=DF,
∴四边形BEFD是正方形,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目