题目内容
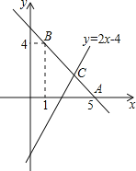
【题目】一次函数y1=﹣2x+b的图象交x轴于点A、与正比例函数y2=2x的图象交于点M(m,m+2),
(1)求点M坐标;
(2)求b值;
(3)点O为坐标原点,试确定△AOM的形状,并说明你的理由.
【答案】(1)M坐标(2,4);(2)b=8;(3)△AOM是等腰三角形,理由见解析
【解析】
(1)把点M的坐标代入正比例函数关系式可得关于m的方程,解方程即可求出m,进而可得答案;
(2)把(1)题中求得的点M坐标代入一次函数的关系式即可求得结果;
(3)易求点A的坐标,然后可根据两点间的距离公式和勾股定理依次求出OA,AM,OM的长,进而可得结论.
解:(1)把点M(m,m+2)代入y2=2x得:m+2=2m,解得:m=2,
∴点M坐标(2,4);
(2)把点M坐标(2,4)代入y1=﹣2x+b中,得:4=﹣2×2+b,解得:b=8;
(3)△AOM是等腰三角形.
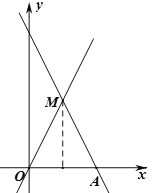
理由:如图,由(2)知,b=8,∴y1=﹣2x+8,
令y=0,则x=4,∴A(4,0),
∴OA=4,AM=![]() ,OM=
,OM=![]() ,
,
∴OM=AM,
∴△AOM是等腰三角形.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目