题目内容
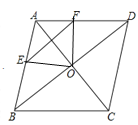
【题目】如图,由6个长为2,宽为1的小矩形组成的大矩形网格,小矩形的顶点称为这个矩形网格的格点,由格点构成的几何图形称为格点图形(如:连接2个格点,得到一条格点线段;连接3个格点,得到一个格点三角形;…),请按要求作图(标出所画图形的顶点字母).
(1)画出4种不同于示例的平行格点线段;

(2)画出4种不同的成轴对称的格点三角形,并标出其对称轴所在线段;

(3)画出1个格点正方形,并简要证明.
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】
(1)根据平行线的判定即可画出图形(答案不唯一);
(2)根据轴对称的性质即可画出图形(答案不唯一);
(3)根据正方形的判定方法即可画出图形(答案不唯一),再根据矩形的性质以及三角形全等的判定与性质进行证明.
解:(1)答案不唯一,如图AB∥CD:

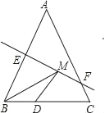
(2)答案不唯一,如图△ABC为所求三角形,虚线为对称轴:
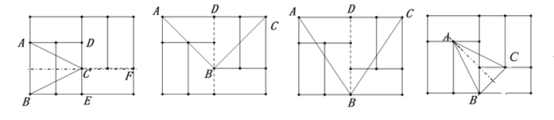
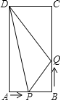
(3)答案不唯一,如图四边形ABCD为正方形:
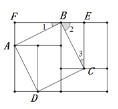
证明:
∵图中所有长方形都全等,
∴AF=BE,∠F=∠BEC=90°,BF=CE,
∴△AFB≌△BEC(SAS),
∴AB=BC,∠1=∠3.
同理,易得AB=AD=DC,
∴四边形ABCD为菱形.
∵∠1=∠3,
∴∠1+∠2=90°,
∴∠ABC=90°,
∴四边形ABCD为正方形.

练习册系列答案
相关题目