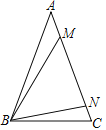题目内容
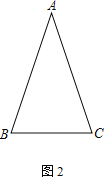
【题目】如图,在等腰△ABC中,AC=BC,D,E分别为AB,BC上一点,∠CDE=∠A.
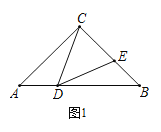
(1)如图1,若BC=BD,∠ACB=90°,则∠DEC度数为_________°;
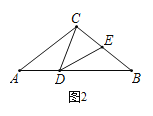
(2)如图2,若BC=BD,求证:CD=DE;
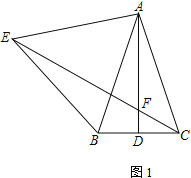
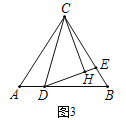
(3)如图3,过点C作CH⊥DE,垂足为H,若CD=BD,EH=1,求DE-BE的值.
【答案】(1)67.5;(2)证明见解析;(3)DE-BE=2.
【解析】
(1)先根据等腰三角形的性质,得出∠A=∠B=45°=∠CDE,再根据BC=BD,可得出∠BDC的度数,然后可得出∠BDE的度数,最后根据三角形外角的性质可得出∠DEC的度数;
(2)先根据条件得出∠ACD=∠BDE,BD=AC,再根据ASA判定△ADC≌△BED,即可得到CD=DE;
(3)先根据条件得出∠DCB=∠CDE,进而得到CE=DE,再在DE上取点F,使得FD=BE,进而判定△CDF≌△DBE(SAS),得出CF=DE=CE,再根据CH⊥EF,运用三线合一即可得到FH=HE,最后得出CE-BE=DE-DF=EF=2HE,即可得出结论.
(1)解:∵AC=BC,∠ACB=90°,
∴∠A=∠B=45°=∠CDE,
又BC=BD,
∴∠BDC=∠BCD=![]() (180°-∠B)=67.5°,
(180°-∠B)=67.5°,
∴∠BDE=∠BDC-∠CDE=67.5°-45°=22.5°,
∴∠DEC=∠B+∠BDE=67.5°;
故答案为:67.5;
(2)证明:∵AC=BC,∠CDE=∠A,
∴∠A=∠B=∠CDE,
∵∠CDB=∠A+∠ACD=∠CDE+∠BDE,
∴∠ACD=∠BDE,
又∵BC=BD,
∴BD=AC,
在△ADC和△BED中,
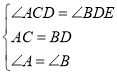 ,
,
∴△ADC≌△BED(ASA),
∴CD=DE;
(3)解:∵CD=BD,
∴∠B=∠DCB,
由(2)知:∠CDE=∠B,
∴∠DCB=∠CDE,
∴CE=DE,
如图,在DE上取点F,使得FD=BE,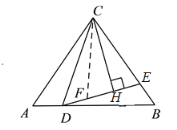
在△CDF和△DBE中,
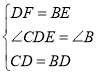 ,
,
∴△CDF≌△DBE(SAS),
∴CF=DE=CE,
又∵CH⊥EF,
∴FH=HE,
∴DE-BE=DE-DF=EF=2HE=2.