题目内容
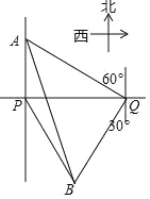
【题目】一轮船在P处测得灯塔A在正北方向,灯塔B在南偏东30°方向,轮船向正东航行了900m,到达Q处,测得A位于北偏西60°方向, B位于南偏西30°方向.
(1)线段BQ与PQ是否相等?请说明理由;
(2)求A、B间的距离(结果保留根号).
【答案】(1)相等;(2)![]()
【解析】试题分析:(1)由题意知∠QPB=60°、∠PQB=60°,从而得△BPQ是等边三角形,据此可得答案;
(2)由(1)知PQ=BQ=900m,从而得AQ=![]() ,根据∠AQB=180°-60°-30°=90°知AB=
,根据∠AQB=180°-60°-30°=90°知AB=![]() (m).
(m).
试题解析:(1)相等,由图知∠QPB=60°、∠PQB=60°,
∴△BPQ是等边三角形,∴BQ=PQ;
(2)由(1)知PQ=BQ=900m,在Rt△APQ中,AQ=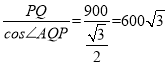 ,
,
又∵∠AQB=180°﹣60°﹣30°=90°,
∴在Rt△AQB中,AB=![]() (m),
(m),
答:A、B间的距离为300![]() m.
m.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目