题目内容
【题目】曲阜限制“三小车辆”出行后,为方便市民出行,准备为![]() 、
、![]() 、
、![]() 、
、![]() 四个村建一个公交车站
四个村建一个公交车站![]() .
.
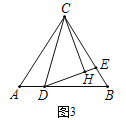
(1)请问:公交站![]() 建在何处才能使它到4个村的距离之和
建在何处才能使它到4个村的距离之和![]() 最小,请在图一中找出点
最小,请在图一中找出点![]() ;
;
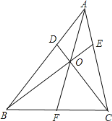
(2)请问:公交站![]() 建在何处才能使它到道路
建在何处才能使它到道路![]() 、
、![]() 、
、![]() 的距离相等,请在图二中找出点
的距离相等,请在图二中找出点![]() 并加以说明.
并加以说明.
【答案】(1)见解析;(2)见解析
【解析】
(1)公交站P是AC与BD的交点,要证这点到四点的距离最小,可以证明除这点以外的点到四点的距离大于这点到四点的距离;
(2)公交站![]() 是∠ABC与∠DCB角平分线的交点,由角平分线性质定理可知,角平分线上的点到这个角两边的距离相等.
是∠ABC与∠DCB角平分线的交点,由角平分线性质定理可知,角平分线上的点到这个角两边的距离相等.
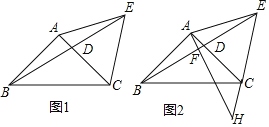
解:(1)应建在AC,BD连线的交点P处,如图一,

理由:如下图,若不建在P处,建在P1处,由三角形两边之和大于第三边可知,
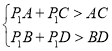 ,
,
即P1A+P1C+P1B+P1D>AC+BD,
故结论成立应建在P处.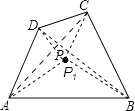
即P1A+P1C+P1B+P1D>AC+BD.
故结论成立应建在P处.
(2)应建在∠ABC与∠DCB角平分线的交点处,如图二,
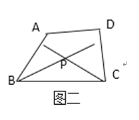
理由:由角平分线性质定理可知,角平分线上的点到这个角两边的距离相等.
所以点P道路![]() 、
、![]() 、
、![]() 的距离相等.
的距离相等.

练习册系列答案
相关题目
【题目】[问题情境]
已知矩形的面积为一定值1,当该矩形的一组邻边分别为多少时,它的周长最小?最小值是多少?
[数学模型]
设该矩形的一边长为x,周长为L,则L与x的函数表达式为 .
[探索研究]
小彬借鉴以前研究函数的经验,先探索函数![]() 的图象性质.
的图象性质.
(1)结合问题情境,函数![]() 的自变量x的取值范围是 ,
的自变量x的取值范围是 ,
如表是y与x的几组对应值.
x | … |
|
|
| 1 | 2 | 3 | m | … |
y | … | 4 | 3 | 2 | 2 | 2 | 3 | 4 | … |
①直接写出m的值;
②画出该函数图象,结合图象,得出当x= 时,y有最小值,y的最小值为 .
[解决问题]
(2)直接写出“问题情境”中问题的结论.