Question

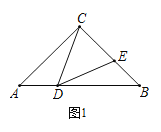
【题目】如图，在△ABC中，AB＝AC，∠ABM＝∠CBN，MN＝BN，则∠MBC的度数为_________°．

Answer 1

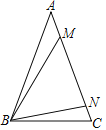
【答案】60

【解析】

可设∠ABM=∠CBN=α，∠MBN=∠BMN=β，利用三角形外角的性质，得出β=α+∠A，而∠C=∠ABC=2α+β，结合三角形内角和定理可求出β+α=60°，即可得出∠MBC的度数．

解：设∠ABM=∠CBN=α，
∵BN=MN，可设∠MBN=∠BMN=β，
∵∠BMN是△ABM的外角，
∴∠BMN=α+∠A，
即β=α+∠A，∴∠A=β-α，
∵AB=AC，
∴∠ABC=∠C=2α+β，
∵∠A+∠B+∠C=180°，

∴β-α+2（2α+β）=180°，
∴β+α=60°，

∴∠MBC=β+α=60°．

故答案为：60．