Question

【题目】如图，在四边形ABCD中，对角线AC、BD相交于点O，若BC=4，AO=CO=3，BD=10，∠ACB=90°，求AD的长及四边形ABCD的面积．

Answer 1

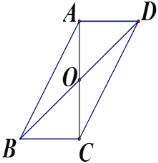
【答案】4；24

【解析】

由OA=OC=3，∠ACB=90°，BC=4，利用勾股定理可以求出OB的长，再根据BD=10，即可求出OD的长，进而证明△AOD≌△COB，从而得到AD=CB，∠OAD=∠OCB=90°，进而可以得到AD的长及四边形ABCD的面积．

∵OA=OC=3，∠ACB=90°，BC=4，

∴OB=5，AC=6，

∵BD=10，

∴OB=OD=5，

在△AOD和△COB中，

,

∴△AOD≌△COB（SAS），

∴AD=CB，∠OAD=∠OCB=90°，

∵CB=4，

∴AD=4，

∵四边形ABCD的面积是：

即AD的长是4，四边形ABCD的面积是24．