题目内容
【题目】(1)阅读思考:
小迪在学习过程中,发现“数轴上两点间的距离”可以用“表示这两点数的差”来表示,探索过程如下:
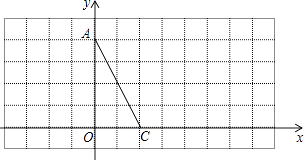
如图1所示,线段AB,BC,CD的长度可表示为:AB=3=4﹣1,BC=5=4﹣(﹣1),CD=3=(﹣1)﹣(﹣4),于是他归纳出这样的结论:如果点A表示的数为a,点B表示的数为b,当b>a时,AB=b﹣a(较大数﹣较小数).

(2)尝试应用:
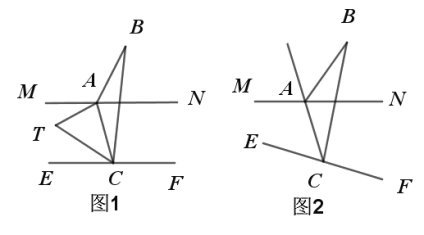
①如图2所示,计算:OE= ,EF= ;
②把一条数轴在数m处对折,使表示﹣19和2019两数的点恰好互相重合,则m= ;

(3)问题解决:
①如图3所示,点P表示数x,点M表示数﹣2,点N表示数2x+8,且MN=4PM,求出点P和点N分别表示的数;
②在上述①的条件下,是否存在点Q,使PQ+QN=3QM?若存在,请直接写出点Q所表示的数;若不存在,请说明理由.

【答案】(2)①5,8;②1000;(3)①点 P表示的数为﹣3,点 N表示的数为2;②﹣5或﹣![]()
【解析】
(2)尝试应用:①利用得出的结论直接计算即可;
②利用对称的性质列方程解答即可;
(3)问题解决:①根据图表示的数,利用MN=4PM,建立方程求得答案;
②设出点D表示的数,根据题意列出方程探讨得出答案即可.
(2)尝试应用:
①OE=0-(-5)=5,EF=3-(-5)=8,
②m﹣(﹣19)=2019﹣m,
解得m=1000;
故答案为:5,8,1000;
(3)问题解决:
①∵MN=2x+8﹣(﹣2),PM=﹣2﹣x,
∵MN=4PM,
∴2x+10=4(﹣2﹣x),
∴x=﹣3,2x+8=2
∴点 P表示的数为﹣3,点 N表示的数为2;
②存在,分析题意可知Q只能在P点左侧或者在MN之间,设点Q表示的数为a,
当Q在P点左侧时:根据题意得:﹣3﹣a+2﹣a=3(﹣2﹣a)解得a=﹣5;当点Q在MN之间时:a+3+2﹣a=3(a+2),
解得a=﹣![]() ;
;
故点Q表示的数为﹣5或﹣![]() .
.

【题目】重庆市居民用水的水价实行阶梯收费,标准如下表:
每户居民每月用水量 | 水费单价(元) |
|
|
|
|
| 4.5 |
(1)已知张三家5月份用水13吨,缴费47元,6月份用水15吨,缴费55元.请根据上述信息,求![]() 、
、![]() 的值.
的值.
(2)在(1)的条件下,由于天气变热,7月份是用水高峰期,张三家计划7月份水费支出不超过100元,那么张三家7月份最多可用多少吨水?
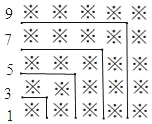
【题目】为了解某校创新能力大赛的笔试情况,随机抽查了部分参赛同学的成绩,整理井制作了不完整的统计表和统计图,请根据图表中提供的信息解答问题:
分数x(分) | 频数 | 百分比 |
60≤x<70 | 30 | 10% |
70≤x<80 | 90 | n |
80≤x<90 | m | 40% |
90≤x<100 | 60 | 20% |
(1)本次调查统计的学生人数为多少.
(2)在表中:写出m,n的值.
(3)补全频数分布直方图.