题目内容
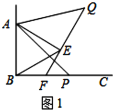
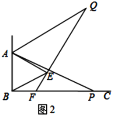
【题目】如图,正方形ABCD顶点A,D在⊙O上,边BC经过⊙O上一定P,且PF平分∠AFC,边 AB,CD分别与⊙O相交于点E,F,连接EF.
(1)求证:BC是⊙O的切线;
(2)若FC=2,求PC的长.
【答案】
(1)证明:连接OP,
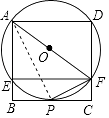
∵四边形ABCD是正方形,
∴∠B=∠C=∠D=90°,AB=BC,
∵PF平分∠AFC,
∴∠AFP=∠PFC,
∵OP=OF,
∴∠AFP=∠OPF,
∴∠PFC=∠OPF,
∴OP∥CD,
∴∠BPO=∠C=90°,
∴OP⊥BC,
∴BC是⊙O的切线;
(2)解:连接AP,∵∠D=90°,∴AF是⊙O的直径,
∴∠AEF=∠APF=90°,
∴∠BEF=∠B=∠C=90°,
∵OP∥CD,∴OP∥CD∥BA,
∴ ![]() ,
,
∴BP= ![]() BC=
BC= ![]() BA,
BA,
∵∠APB+∠FPC=90°,∠PFC+∠FPC=90°,
∴∠APB=∠PFC,
∵∠B=∠C=90°,
∴△APB∽△PFC,
∴ ![]() ,∴
,∴ ![]() ,
,
∴PC=2FC=4.
【解析】(1)连接OP,依据等腰三角形的性质可证明∠OPF=∠OFP,然后结合角平分线的定义可得到∠OPF=∠PFC,接下来,可证明OP∥FC,最后,平行线的性质可证明OP⊥BC;
(2)连接AP,首先证明△APB∽△PFC,然后再依据相似三角形对应边成比例列出比例式求解即可.
【考点精析】通过灵活运用正方形的性质,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形即可以解答此题.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目