题目内容
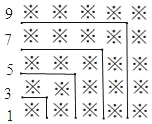
【题目】探索规律,观察下面由※组成的图案和算式,并解答问题.
1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
(1)试写出1+3+5+7+9+…+19= ;
(2)试写出1+3+5+7+9+…+(2n﹣1)= ;
(3)请用上述规律计算:
①101+103+105+107+…+2017+2019;
②(2m+1)+(2m+3)+(2m+5)+…+(2n+7)(其中n>m)(列出代数式即可)
【答案】(1)100;(2)n2;(3)①1017600;②(n+4)2﹣m2
【解析】
(1)(2)观察不难发现,从1开始的连续奇数的和等于首尾两个奇数的和的一半的平方,根据此规律进行计算即可得解;
(3)①用从1开始到2019的连续奇数的和减去从1开始到99的连续奇数的和,然后根据规律进行计算即可得解;
②用从1开始到(2n+7)的连续奇数的和减去从1开始到(2m﹣1)的连续奇数的和,然后根据规律进行计算即可得解.
解:(1)![]()
故答案为100;
(2)![]()
故答案为:n2;
(3)①101+103+105+107+…+2017+2019
=(1+3+5+7+9+…+2019)﹣(1+3+5+7+9+…+99)
![]()
=10102﹣502
=1020100﹣2500
=1017600;
②(2m+1)+(2m+3)+(2m+5)+…+(2n+7)
=[1+3+5+7+9+…+(2n+7)]﹣[1+3+5+7+9+…+(2m﹣1)]
![]()
=(n+4)2﹣m2.

【题目】把正方体的6个面分别涂上不同的颜色,并画上朵数不等的花,各面上的颜色与花朵数的情况如下表:
颜色 | 红 | 黄 | 蓝 | 白 | 紫 | 绿 |
花朵数 | 1 | 2 | 3 | 4 | 5 | 6 |
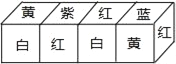
现将上述大小相同,颜色、花朵分布完全一样的四个正方体拼成一个在同一平面上放置的长方体,如图所示,那么长方体的下底面共有_____朵花.
【题目】为了鼓励市民节约用水,万州市居民生活用水按阶梯式水价计费,表是该市居民“一户一表”生活用水阶梯式计费价格表的一部分信息:(水价计费![]() 自来水销售费用
自来水销售费用![]() 污水处理费用)
污水处理费用)
自来水销售价格 | 污水处理价格 | |
每户每月用水量 | 单价:元 | 单价:元 |
17吨及以下 |
| 0.80 |
超过17吨不超过30吨的部分 |
| 0.80 |
超过30吨的部分 | 6.00 | 0.80 |
说明:①每户产生的污水量等于该户的用水量,②水费=自来水费+污水处理费;
已知小明家2013年3月份用水20吨,交水费66元;5月份用水25吨,交水费91元.
(1)求![]() ,
,![]() 的值.
的值.
(2)随着夏天的到来,用水量将增加。为了节省开支,小梦计划把6月份的水费控制在不超过家庭月收入的2%,若小梦加的月收入为9200元,则小王家6月份最多能用水多少吨?