ЬтФПФкШн
ЁОЬтФПЁПЁЖКЏЪ§ЕФЭМЯѓгыаджЪЁЗЭиеЙбЇЯАеЙЪОЃК
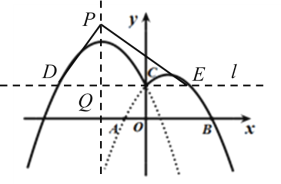
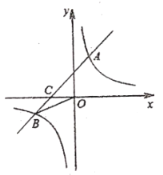
ЃЈЮЪЬтЃЉШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпG1ЃК![]() гыxжсЯрНЛгкAЃЈ-1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкЕуCЃЌдђa= ЃЌb= ЃЎ
гыxжсЯрНЛгкAЃЈ-1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкЕуCЃЌдђa= ЃЌb= ЃЎ
ЃЈВйзїЃЉНЋЭМ1жаХзЮяЯпG1биBCЗНЯђЦНвЦBCГЄЖШЕФОрРыЕУЕНХзЮяЯпG2ЃЌG2дкyжсзѓВрЕФВПЗжгыG1дкyжсгвВрЕФВПЗжзщГЩЕФаТЭМЯѓМЧЮЊGЃЌШчЭМЂкЃЎЧыжБНгаДГіЭМЯѓGЖдгІЕФКЏЪ§НтЮіЪНЃЎ
ЃЈЬНОПЃЉдкЭМ2жаЃЌЙ§ЕуCзїжБЯпlЦНаагкxжсЃЌгыЭМЯѓGНЛгкDЃЌEСНЕуЃЎЧѓЭМЯѓGдкжБЯпlЩЯЗНЕФВПЗжЖдгІЕФКЏЪ§yЫцxЕФдіДѓЖјдіДѓЪБxЕФШЁжЕЗЖЮЇЃЎ
ЃЈгІгУЃЉPЪЧХзЮяЯпG2ЖдГЦжсЩЯвЛИіЖЏЕуЃЌЕБЁїPDEЪЧжБНЧШ§НЧаЮЪБЃЌжБНгаДГіPЕуЕФзјБъЃЎ

ЁОД№АИЁПЮЪЬтЃК![]() ЃЌ1ЃЛВйзїЃК
ЃЌ1ЃЛВйзїЃК ЃЛЬНОПЃК-4ЃМxЃМ-2Лђ0ЃМxЃМ1ЃЛгІгУЃКЃЈ-2ЃЌ
ЃЛЬНОПЃК-4ЃМxЃМ-2Лђ0ЃМxЃМ1ЃЛгІгУЃКЃЈ-2ЃЌ![]() +
+![]() ЃЉЛђЃЈ-2ЃЌ
ЃЉЛђЃЈ-2ЃЌ![]() -
-![]() ЃЉ.
ЃЉ.
ЁОНтЮіЁП
ЮЪЬтЃКРћгУД§ЖЈЯЕЪ§ЗЈНЋAКЭBЕФзјБъДњШыЃЌЧѓГіaКЭbЕФжЕМДПЩЃЛ
ВйзїЃКИљОнЬтвтЧѓГіЦНвЦКѓЕФХзЮяЯпG2ЕФБэДяЪНЃЌНсКЯG1ЕФБэДяЪНМДПЩЕУГіНсЙћЃЛ
ЬНОПЃКЛГіЭМЯёЃЌЧѓГіСНВПЗжЕФХзЮяЯпЕФЖдГЦжсЃЌвдМАDКЭEЕФзјБъЃЌНсКЯПЊПкЗНЯђЃЌПЩЕУxЕФШЁжЕЗЖЮЇЃЛ
гІгУЃКгЩЬтвтХаЖЯГіЁЯDPE=90ЁуЃЌдкЁїDPEжаРћгУЙДЙЩЖЈРэЧѓГіPQЕФГЄЃЌДгЖјЕУГіЕуPзјБъ.
НтЃКЮЪЬтЃКЁпХзЮяЯп![]() гыxжсНЛгкAЃЈ-1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉСНЕуЃЌ
гыxжсНЛгкAЃЈ-1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉСНЕуЃЌ
Ёр ЃЌ
ЃЌ
НтЕУЃК ЃЌ
ЃЌ
ЙЪД№АИЮЊЃК![]() ЃЌ1ЃЛ
ЃЌ1ЃЛ
ВйзїЃКЁпХзЮяЯпG1биBCЗНЯђЦНвЦBCГЄЖШЕФОрРыЕУЕНХзЮяЯпG2ЃЌ
BЃЈ3,0ЃЉЃЌCЃЈ0ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ![]() ЃЌ
ЃЌ
ЁрЦНвЦКѓЕФХзЮяЯпG2ЕФБэДяЪНЮЊ![]() ЃЌ
ЃЌ
ЁпG2дкyжсзѓВрЕФВПЗжгыG1дкyжсгвВрЕФВПЗжзщГЩЕФаТЭМЯѓМЧЮЊGЃЌ
ЁрЭМЯёGЕФНтЮіЪНЮЊ ЃЛ
ЃЛ
ЬНОПЃКгЩЬтвтПЩЕУЃКЕБxЁн0ЪБЃЌ![]() ЃЌПЊПкЯђЯТЃЌЖдГЦжсЮЊжБЯпx=1ЃЌ
ЃЌПЊПкЯђЯТЃЌЖдГЦжсЮЊжБЯпx=1ЃЌ
Сюy=0ЃЌНтЕУЃКx1=0ЃЌx2=2ЃЌ
ЁрEЃЈ2ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрЕБ0ЃМxЃМ1ЪБЃЌyЫцxдіДѓЖјдіДѓЃЛ
ЕБxЃМ0ЪБЃЌ![]() ЃЌПЊПкЯђЯТЃЌЖдГЦжсЮЊжБЯпx=-2ЃЌ
ЃЌПЊПкЯђЯТЃЌЖдГЦжсЮЊжБЯпx=-2ЃЌ
Сюy=0ЃЌНтЕУЃКx1=-4ЃЌx2=0ЃЌ
ЁрЕуDЃЈ-4ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрЕБ-4ЃМxЃМ-2ЪБЃЌyЫцxдіДѓЖјдіДѓЃЛ
злЩЯЃКЭМЯѓGдкжБЯпlЩЯЗНЕФВПЗжЖдгІЕФКЏЪ§yЫцxЕФдіДѓЖјдіДѓЪБЃЌ
xЕФШЁжЕЗЖЮЇЪЧЕБ-4ЃМxЃМ-2Лђ0ЃМxЃМ1ЃЛ
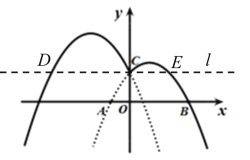
гІгУЃКЁпЁїPDEЪЧжБНЧШ§НЧаЮЃЌPЪЧХзЮяЯпG2ЖдГЦжсЩЯвЛИіЖЏЕуЃЌ
ЁржЛДцдкЁЯDPE=90ЁуЃЌ
гЩЬтвтЕУЃКDЃЈ-4ЃЌ![]() ЃЉЃЌEЃЈ2ЃЌ
ЃЉЃЌEЃЈ2ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЕБЕуPдкжБЯпlЩЯЗНЪБЃЌШчЭМЃЌЩшжБЯпlгыG2ЕФЖдГЦжсНЛгкЕуQЃЌ
ПЩЕУQЃЈ-2ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрDQ=2ЃЌQE=4ЃЌDE=6ЃЌPQЁЭDEЃЌ
ЩшPQ=mЃЌдкЁїPDQКЭЁїPEQжаЃЌ
PQ2+DQ2=PD2ЃЌPQ2+QE2=PE2ЃЌ
МД![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
дкЁїPDEжаЃЌPD2+PE2=DE2ЃЌ
МД![]() ЃЌ
ЃЌ
НтЕУЃКm=![]() Лђm=
Лђm=![]() ЃЈЩсЃЉЃЌ
ЃЈЩсЃЉЃЌ
Ёрm+![]() =
=![]() +
+![]() ЃЌ
ЃЌ
ЁрЕуPЕФзјБъЮЊЃЈ-2ЃЌ![]() +
+![]() ЃЉЃЌ
ЃЉЃЌ
ЕБЕуPдкжБЯпlЯТЗНЪБЃЌЭЌРэPQ=![]() ЃЌ
ЃЌ
ДЫЪБЕуPЕФзјБъЮЊЃЈ-2ЃЌ![]() -
-![]() ЃЉЃЌ
ЃЉЃЌ
злЩЯЃКЕуPЕФзјБъЮЊЃЈ-2ЃЌ![]() +
+![]() ЃЉЛђЃЈ-2ЃЌ
ЃЉЛђЃЈ-2ЃЌ![]() -
-![]() ЃЉ.
ЃЉ.