ЬтФПФкШн
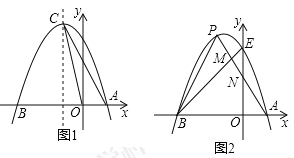
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=Љx2+bx+cЕФЭМЯѓгыxжсНЛгкA(Љ4ЃЌ0)КЭЕуBСНЕуЃЌгыyжсНЛгкЕуCЃЌХзЮяЯпЕФЖдГЦжсЪЧx=Љ1гыxжсНЛгкЕуDЃЎ
ЃЈ1ЃЉЧѓЮяЯпЕФКЏЪ§БэДяЪНЃЛ
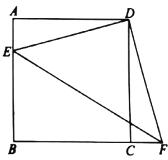
ЃЈ2ЃЉШєЕуP(mЃЌn)ЮЊХзЮяЯпЩЯвЛЕуЃЌЧвЉ4ЃМmЃМЉ1ЃЌЙ§ЕуPзїPEЁЮxжсЃЌНЛХзЮяЯпЕФЖдГЦжсx=Љ1гкЕуEЃЌзїPFЁЭxжсгкЕуFЃЌЕУЕНОиаЮPEDFЃЌЧѓОиаЮPEDFжмГЄЕФзюДѓжЕЃЛ
ЃЈ3ЃЉЕуQЮЊХзЮяЯпЖдГЦжсx=Љ1ЩЯвЛЕуЃЌЪЧЗёДцдкЕуQЃЌЪЙвдЕуQЃЌBЃЌCЮЊЖЅЕуЕФШ§НЧаЮЪЧжБНЧШ§НЧаЮЃПШєДцдкЃЌЧыжБНгаДГіЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉy=Љx2Љ2x+8ЃЛЃЈ2ЃЉЕБm=Љ![]() ЪБЃЌОиаЮPEDFЕФжмГЄгазюДѓжЕЪЧ
ЪБЃЌОиаЮPEDFЕФжмГЄгазюДѓжЕЪЧ![]() ЃЛЃЈ3ЃЉДцдкЃЌЕуQ (Љ1ЃЌ
ЃЛЃЈ3ЃЉДцдкЃЌЕуQ (Љ1ЃЌ![]() )Лђ(Љ1ЃЌЉ
)Лђ(Љ1ЃЌЉ![]() )Лђ(Љ1ЃЌ4+
)Лђ(Љ1ЃЌ4+![]() )Лђ(Љ1ЃЌ4Љ
)Лђ(Љ1ЃЌ4Љ![]() )ЃЎ
)ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнХзЮяЯпЖдГЦжсЙЋЪНЧѓbЕФжЕЃЌШЛКѓНЋAЕузјБъДњШыНтЮіЪНЧѓcЕФжЕЃЌДгЖјЧѓНтЃЛ
ЃЈ2ЃЉЩшPЕузјБъЮЊ(mЃЌn)ЃЌгЩЬтвтnЈTЉm2Љ2m+8ЃЌДгЖјБэЪОГіОиаЮжмГЄЕФКЏЪ§ЙиЯЕЪНЃЌШЛКѓРћгУЖўДЮКЏЪ§ЕФаджЪЧѓзюжЕЃЛ
ЃЈ3ЃЉЩшQ(Љ1ЃЌy)ЃЌНсКЯЭМаЮгУЙДЙЩЖЈРэЗжБ№БэЪОГіQB2 =9+y2ЃЌQC2=1+(yЉ8)2ЃЌBC2=68ЃЌШЛКѓЗжЁЯQCB=90ЁуЃЌЁЯQBC=90ЁуЃЌЁЯBQC=90ЁуШ§жжЧщПіСаЗНГЬЧѓНтЃЌДгЖјШЗЖЈЕуQзјБъЃЎ
НтЃКЃЈ1ЃЉЁпХзЮяЯпy=Љx2+bx+cЕФЖдГЦжсЪЧx=Љ1ЃЌ
ЁрЉ![]() =Љ1ЃЌb=Љ2ЃЌ
=Љ1ЃЌb=Љ2ЃЌ
Ёрy=Љx2Љ2x+cЃЌ
АбA(Љ4ЃЌ0)ДњШыЕУЃКЉ16+8+c=0ЃЌЁрc=8ЃЌ
ЁрЮяЯпЕФКЏЪ§БэДяЪНЮЊЃКy=Љx2Љ2x+8ЃЛ
ЃЈ2ЃЉЁпЕуP(mЃЌn)ЮЊХзЮяЯпЩЯвЛЕуЃЌЧвЉ4ЃМmЃМЉ1ЃЌШчЭМ1ЃЌ
 ЃЌ
ЃЌ
ЁрnЈTЉm2Љ2m+8ЃЎ
ЁпЫФБпаЮPEDFЪЧОиаЮЃЌ
ЁрОиаЮPEDFЕФжмГЄ=2PE+2PF
=2(Љ1Љm)+2(Љm2Љ2m+8)
=Љ2m2Љ6m+14
=Љ2(m+![]() )2+
)2+![]() ЃЎ
ЃЎ
ЁпЉ2ЃМ0ЃЌЁрЕБm=Љ![]() ЪБЃЌОиаЮPEDFЕФжмГЄгазюДѓжЕЪЧ
ЪБЃЌОиаЮPEDFЕФжмГЄгазюДѓжЕЪЧ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉДцдкЕуQЃЌЪЙвдЕуQЃЌBЃЌCЮЊЖЅЕуЕФШ§НЧаЮЪЧжБНЧШ§НЧаЮЃЎ
ЁпЕуQЮЊХзЮяЯпЖдГЦжсx=Љ1ЩЯвЛЕуЃЌЁрЩшQ(Љ1ЃЌy)ЃЌ
гЩЖдГЦЕУЃКB(2ЃЌ0)ЃЎ
ЁпC(0ЃЌ8)ЃЌ
ЁрQB2=(2+1)2+y2=9+y2ЃЌQC2=(Љ1)2+(yЉ8)2=1+(yЉ8)2ЃЌBC2=22+82=4+64=68ЃЌ
ЗжШ§жжЧщПіЃК
ЂйЕБЁЯQCB=90ЁуЪБЃЌQBЪЧаББпЃЌЁрQB2=QC2+BC2ЃЌЁр9+y2=1+(yЉ8)2+68
НтЕУЃКy=![]() ЃЌ
ЃЌ
ЁрQ(Љ1ЃЌ![]() )ЃЛ
)ЃЛ
ЂкЕБЁЯQBC=90ЁуЪБЃЌQCЪЧаББпЃЎ
ЁпQC2=BC2+QB2ЃЌЁр1+(yЉ8)2=68+9+y2ЃЌ
НтЕУЃКy=Љ![]() ЃЌ
ЃЌ
ЁрQ(Љ1ЃЌЉ![]() )ЃЛ
)ЃЛ
ЂлЕБЁЯBQC=90ЁуЪБЃЌBCЪЧаББпЃЎ
ЁпBC2=BQ2+QC2ЃЌЁр68=1+(yЉ8)2+9+y2ЃЌ
НтЕУЃКy=4ЁР![]() ЃЌЁрQ(Љ1ЃЌ4+
ЃЌЁрQ(Љ1ЃЌ4+![]() )Лђ(Љ1ЃЌ4Љ
)Лђ(Љ1ЃЌ4Љ![]() )ЃЛ
)ЃЛ
злЩЯЃЌЕуQЕФзјБъЪЧ(Љ1ЃЌ![]() )Лђ(Љ1ЃЌЉ
)Лђ(Љ1ЃЌЉ![]() )Лђ(Љ1ЃЌ4+
)Лђ(Љ1ЃЌ4+![]() )Лђ(Љ1ЃЌ4Љ
)Лђ(Љ1ЃЌ4Љ![]() )ЃЎ
)ЃЎ