题目内容
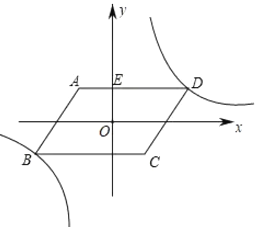
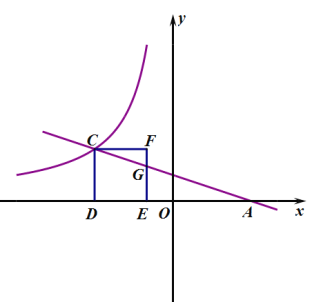
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() 两点,与反比例函数
两点,与反比例函数![]() 交于点
交于点![]() 点
点![]() 的坐标为
的坐标为![]() 轴于点
轴于点![]() .
.

(1)点![]() 的坐标为 ;
的坐标为 ;
(2)若点![]() 为
为![]() 的中点,求反比例函数
的中点,求反比例函数![]() 的解析式;
的解析式;
(3)在(2)条件下,以![]() 为边向右作正方形
为边向右作正方形![]() 交
交![]() 于点
于点![]() 直接写出
直接写出![]() 的周长与
的周长与![]() 的周长的比.
的周长的比.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)将点A代入一次函数,从而得出一次函数的解析式,然后再求B点的坐标;
(2)根据题意,OB是△ACD的中位线,利用中位线的性质可得点C的坐标,代入反比例函数可得解析式;
(3)先证△CFG∽△AOB,在根据点的坐标,可求得CD、AO的长,根据相似三角形线段比即为周长比解得.
(1)∵一次函数过点A![]() ,代入得:
,代入得:
![]()
解得:b=1
∴一次函数为:![]()
令x=0,则y=1
∴B(0,1)
(2)![]()
![]()
![]() .
.
![]() 点
点![]() 在
在![]() 上
上
![]()
![]()
![]() 反比函数解析式为
反比函数解析式为![]() .
.
(3)![]()
∴CD=2,AO=3
∵四边形CFED是正方形,∴CF=CD=2,CF∥AO,∠F=90°
∴∠FCG=∠BAO
∵∠BOA=∠F=90°
∴△CFG∽△AOB
∴![]() 的周长与
的周长与![]() 的周长的比为:
的周长的比为:![]()
![]()

【题目】2020年2月9日起,受新冠疫情影响,重庆市所有中小学实行“线上教学”,落实教育部“停课不停学”精神.某重点中学初![]() 级为了落实教学常规,特别要求家校联动,共同保证年级
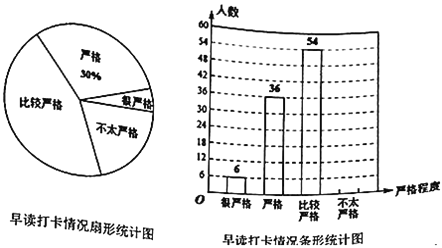
级为了落实教学常规,特别要求家校联动,共同保证年级![]() 名学生上网课期间的学习不受太大影响.为了了解家长配合情况,年级对家长在“钉钉”上早读打卡的严格程度进行了调查,调查结果分为“很严格”,“严格”,“比较严格”和“不太严格”四类.年级抽查了部分家长的调查结果,绘制成如图所示的扇形统计图和条形统计图.
名学生上网课期间的学习不受太大影响.为了了解家长配合情况,年级对家长在“钉钉”上早读打卡的严格程度进行了调查,调查结果分为“很严格”,“严格”,“比较严格”和“不太严格”四类.年级抽查了部分家长的调查结果,绘制成如图所示的扇形统计图和条形统计图.
接着,年级对早读打卡“不太严格”的全体学生进行了第一次基础知识检测,同时召开专题家长会提醒,督促这些家长落实责任,并告知将再次进行检测.两周后,年级又对之前早读打卡“不太严格”的这部分学生进行了第二次基础知识检测.
[整理、描述数据]
以下是抽查的家长打卡“不太严格”的对应学生的两次检测(满分均为![]() 分)情况:
分)情况:
分数段 |
|
|
|
|
|
第一次人数 |
|
|
|
|
|
第二次人数 |
|
|
|
|
|
[分析数据]:
众数 | 中位数 | 平均数 | |
第一次 |
|
|
|
第二次 |
|
|
|
请根据调查的信息
(1)本次参与调查的学生总人数是___,并补全条形统计图;
(2)计算![]() ____,
____,![]() ____,并请你估计全年级所有被检测学生中,第二次检测得分不低于
____,并请你估计全年级所有被检测学生中,第二次检测得分不低于![]() 分的人数;
分的人数;
(3)根据调查的相关数据,请选择适当的统计量评价学校对早读打卡“不太严格”的家长召开专题家长会的效果.