题目内容
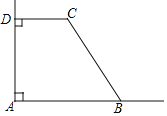
【题目】如图所示，AB⊥AD于点A，CD⊥AD于点D，∠C＝120°．若线段BC与CD的和为12，则四边形ABCD的面积可能是（ ）
A.24
B.30C.45D.
【答案】A
【解析】
过C作CH⊥AB于H，推出四边形ADCH是矩形，四边形ABCD是直角梯形，求得∠BCH＝30°，设BC＝x，则CD＝12﹣x，得到AH＝12﹣x，BH＝
x，CH＝
x，根据梯形的面积公式和二次函数的性质即可得到结论．
解：过C作CH⊥AB于H，
∵AB⊥AD，CD⊥AD，
∴∠A＝∠ADC＝∠AHC＝90°，CD∥AB，
∴四边形ADCH是矩形，四边形ABCD是直角梯形，
∴∠DCH＝90°，CD＝AH，
∵∠BCD＝120°，
∴∠BCH＝30°，
设BC＝x，则CD＝12﹣x，
∴AH＝12﹣x，BH＝x，CH＝x，
∴四边形ABCD的面积＝（CD+AB）CH＝（12﹣x+12﹣x+x）×x，
∴四边形ABCD的面积＝﹣
（x﹣8）2+24
，
∴当x＝8时，四边形ABCD的面积有最大值24，
即四边形ABCD的面积可能是24，
故选：A．
课时训练江苏人民出版社系列答案【题目】在创客教育理念的指引下，国内很多学校都纷纷建立创客实践及创客空间，致力于从小培养学生的创新精神和创造能力，某校开设了“3D”打印，数学编程，智能机器人，陶艺制作，这四门创客课程，为了了解学生对这四门创客课程的喜爱情况，数学兴趣小组对全校学生进行了随机问卷调查，将调查结果整理后绘制成如下的统计图表：
创客课程 | 频数 | 频率 |
“3D”打印 | 36 | 0.45 |
数学编程 | 0.25 | |
智能机器人 | 16 | b |
陶艺制作 | 8 | |
合计 | a | 1 |
根据图表中提供的信息回答下列问题：
（1）统计表中的a＝________，b＝________；
（2）“陶艺制作”对应扇形的圆心角度数为________；
（3）若该校有学生2000人，请估算全校喜爱“智能机器人”的人数有多少？
