Question

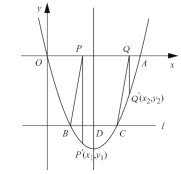
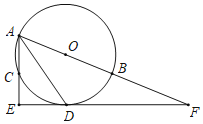
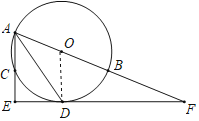
【题目】如图，点A，B，C是半径为2的⊙O上三个点，AB为直径，∠BAC的平分线交圆于点D，过点D作AC的垂线交AC得延长线于点E，延长线ED交AB得延长线于点F．

（1）判断直线EF与⊙O的位置关系，并证明．

（2）若DF=，求tan∠EAD的值．

Answer 1

【答案】（1）直线与圆相切，证明详见解析；（2）

【解析】

（1）连接OD，由OA＝OD知∠OAD＝∠ODA，由AD平分∠EAF知∠DAE＝∠DAO，据此可得∠DAE＝∠ADO，继而知OD∥AE，根据AE⊥EF即可得证；

（2）根据勾股定理得到，根据平行线分线段成比例定理和三角函数的定义即可得到结论．

解：（1）直线与圆相切

理由如下：连接

∵平分

∴

∵

∴

∴

由，得

∵点在圆上

∴是圆的切线

（2）由（1）可得，在中，，，

由勾股定理得

∵

∴

即，得，

∴在中，