题目内容
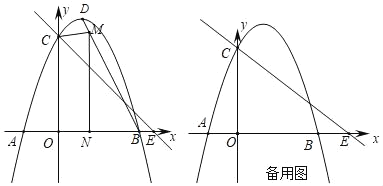
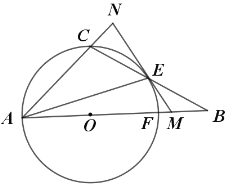
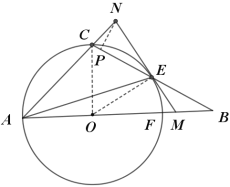
【题目】如图,点O是△ABC中AB边上一点,以点O为圆心,OA的长为半径作⊙O,⊙O恰好经过点C,且与边BC,AB分别交于E,F两点.连接AE,过点E作⊙O的切线,交线段BF于点M,交AC的延长线于点N,且EM=BM,EB=AO.
(1)求![]() 的度数;
的度数;
(2)求证:![]() ;
;
(3)若![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)15°;(2)证明见解析;(3)![]() .
.
【解析】
(1)连接![]() ,则
,则![]() ,由条件得
,由条件得![]() ,求得
,求得![]() ,即可求得
,即可求得![]() ;
;
(2)连接OC,由已知条件可证![]() 为直角三角形,所以
为直角三角形,所以![]() ,即
,即![]() ,通过证明
,通过证明![]() ,得
,得![]() ,
,![]() ,由
,由![]() 进而可证明;
进而可证明;
(3)过点![]() 作
作![]() 于点
于点![]() ,解
,解![]() 得
得![]() ,
,![]() ,由
,由![]() 为等腰直角三角形可求得△NCE为等腰三角形,
为等腰直角三角形可求得△NCE为等腰三角形,![]() ,
,![]() ,由
,由![]() 是等边三角形得
是等边三角形得![]() ,解
,解![]() 得
得![]() ,即可求得三角形面积.
,即可求得三角形面积.
(1)连接![]() ,
,
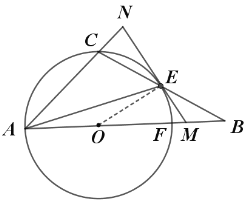
∵直线![]() 与
与![]() 相切于点
相切于点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
∵![]() ,
,
∴![]() ,
,
∵在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]()
∴![]() ,
,
∴![]() ,
,
∴在![]() 中,
中,![]() ;
;
(2)连接![]() ,
,
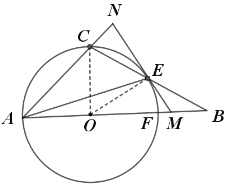
在![]() 中,
中,![]()
∵![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
∵在![]() 中,
中,![]() ,
,
∴在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵由(1)可知:![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
(3)过点![]() 作
作![]() 于点
于点![]() ,
,
∵在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵由(2)可知,![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∵在![]() 中,
中,![]()
![]()
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵由(2)可知,![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∵![]() ,
,
∴在![]() 中
中![]() ,
,
∴![]() .
.

练习册系列答案
相关题目