题目内容
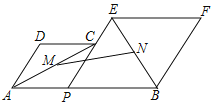
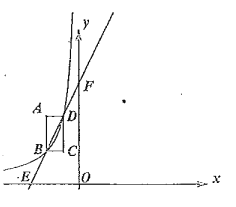
【题目】如图,面积为![]() 的矩形
的矩形![]() 在第二象限,
在第二象限,![]() 与
与![]() 轴平行,反比例函数
轴平行,反比例函数![]() 经过
经过![]() 两点,直线
两点,直线![]() 所在直线
所在直线![]() 与
与![]() 轴、
轴、![]() 轴交于
轴交于![]() 两点,且
两点,且![]() 为线段
为线段![]() 的三等分点,则
的三等分点,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】C
【解析】
延长AB交x轴于点G,延长BC交y轴于点H,根据矩形面积求出![]() 的面积,通过平行可证明
的面积,通过平行可证明![]() ∽
∽![]() ,
,![]() ∽
∽![]() ,
,![]() ∽
∽![]() ,然后利用相似的性质及三等分点可求出
,然后利用相似的性质及三等分点可求出![]() 、
、![]() 、
、![]() 的面积,再求出四边形BGOH的面积,然后通过反比例函数比例系数的几何意义求出k值,再利用
的面积,再求出四边形BGOH的面积,然后通过反比例函数比例系数的几何意义求出k值,再利用![]() 的面积求出b值即可.
的面积求出b值即可.
延长AB交x轴于点G,延长BC交y轴于点H,如图:
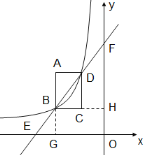
∵矩形ABCD的面积为1,
∴![]() ,
,
∵B、D为线段EF的三等分点,
∴![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ∽
∽![]() ,
,
∴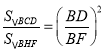 ,即
,即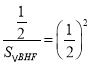 ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ∽
∽![]() ,
,
∴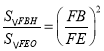 ,即
,即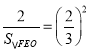 ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ∽
∽![]() ,
,
∴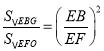 即
即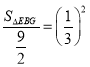 ,
,
∴![]() ,
,
∴![]() ,
,
∵四边形ABCD是矩形,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
又∵![]() ,
,
∴四边形BGOH是矩形,
根据反比例函数的比例系数的几何意义可知:![]() ,
,
∴![]() ,
,
∴![]()
又∵![]() ,即
,即![]() ,
,
∴![]() ,
,
∴直线EF的解析式为![]() ,
,
令![]() ,得
,得![]() ,
,
令![]() ,即
,即![]() ,解得
,解得![]() ,
,
∴![]() ,
,![]() ,
,
∵F点在![]() 轴的上方,
轴的上方,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,即
,即![]() ,
,
∴![]() .
.
故选:C.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案【题目】为了解九年级学生体育水平,学校对九年级全体学生进行了体育测试,并从甲、乙两班中各随机抽取![]() 名学生成绩(满分
名学生成绩(满分![]() 分)进行整理分析(成绩得分用
分)进行整理分析(成绩得分用![]() 表示,共分成四组:
表示,共分成四组:![]()
![]() ;
;![]()
![]() ,
,![]()
![]() )下面给出了部分信息:
)下面给出了部分信息:
甲班![]() 名学生体育成绩:
名学生体育成绩:![]()
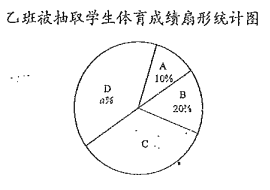
乙班![]() 名学生体育成绩在
名学生体育成绩在![]() 组中的数据是:
组中的数据是: ![]()
甲、乙两班被抽取学生体育成绩统计表
平均数 | 中位数 | 众数 | 方差 | |
甲班 |
|
|
|
|
乙班 |
|
|
|
|
根据以上信息,解答下列问题:
![]() ,
,![]() ,
,![]() ;
;
![]() 根据以上数据,你认为 班(填“甲”或“乙”)体育水平更高,说明理由(两条理由):
根据以上数据,你认为 班(填“甲”或“乙”)体育水平更高,说明理由(两条理由):
![]() ;
;
![]() .
.
![]() 学校九年级学生共
学校九年级学生共![]() 人,估计全年级体育成绩优秀
人,估计全年级体育成绩优秀![]() 的学生人数是多少?
的学生人数是多少?
【题目】已知一个二次函数图象上部分点的横坐标![]() 与纵坐标
与纵坐标![]() 的对应值如表所示:
的对应值如表所示:
| … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
| … | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | … |
(1)求这个二次函数的表达式;
(2)在给定的平面直角坐标系中画出这个二次函数的图象;
(3)当![]() 时,直接写出
时,直接写出![]() 的取值范围.
的取值范围.