题目内容
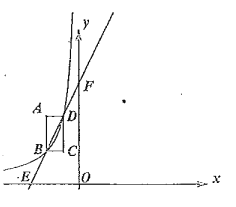
【题目】如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于E,OD⊥BC交⊙O于D,DE交BC于F,点P为CB延长线上的一点,延长PE交AC于G,PE=PF
(1)求证:直线PG为⊙O的切线;
(2)求证:GA=GE;
(3)判断OG与BE的位置关系,并说明理由.
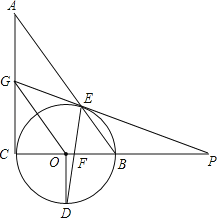
【答案】(1)详见解析;(2)详见解析;(3)OG∥BE,理由详见解析.
【解析】
(1)连接OE,根据等腰三角形的性质得到∠PEF=∠PFE,∠OED=∠ODE,证明∠OEP=90°,根据切线的判定定理证明结论;
(2)根据等腰三角形的性质得到∠OEB=∠OBE,根据对顶角相等得到∠AEG=∠BEP,得到∠AEG=∠A,根据等腰三角形的判定定理证明;
(3)根据切线长定理得到∠OGC=∠OGE,根据三角形的外角性质得到∠OGE=∠AEG,根据平行线的判定定理证明即可.
(1)证明:连接OE,
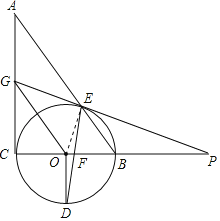
∵PE=PF,
∴∠PEF=∠PFE,
∵OD=OE,
∴∠OED=∠ODE,
∵∠DOF=90°,
∴∠ODE+∠OFD=90°,
∵∠OFD=∠PFE,
∴∠OED+∠PEF=90°,即∠OEP=90°,
∴直线PG为⊙O的切线;
(2)证明:∵OB=OE,
∴∠OEB=∠OBE,
∵∠OEB+∠BEP=90°,
∴∠OBE+∠BEP=90°,
∵∠AEG=∠BEP,
∴∠OBE+∠AEG=90°,
∵∠C=90°,
∴∠OBE+∠A=90°,
∵∠AEG=∠A,
∴GA=GE;
(3)解:OG∥BE,
理由如下:∵GC、GE是⊙O的切线,
∴∠OGC=∠OGE,
∵∠OGC+∠OGE=∠AEG+∠A,∠AEG=∠A,
∴∠OGE=∠AEG,
∴OG∥BE.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某班“数学兴趣小组”对函数![]() 的图象与性质进行了探究,探究过程如下,请补充完整.
的图象与性质进行了探究,探究过程如下,请补充完整.
(1)函数![]() 的自变量
的自变量![]() 的取值范围是_________.
的取值范围是_________.
(2)下表是![]() 与
与![]() 的几组对应值.
的几组对应值.
| … |
|
|
| 0 |
|
| 2 | 3 | 4 | 5 | … |
| … |
|
|
|
|
|
|
|
|
|
| … |
则表格中的![]() __________.
__________.
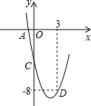
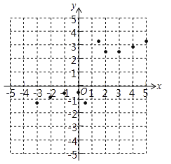
(3)如图,在平面直角坐标系中,描出了以上表格中各组对应值为坐标的点,请根据描出的点,画出该函数的图象;试写出该函数的一条性质________________________________________________________.
(4)①当直线![]() 与函数
与函数![]() 的图象有唯一交点时,
的图象有唯一交点时,![]() 的值为___________;
的值为___________;
②若直线![]() 与函数
与函数![]() 无交点,则
无交点,则![]() 的取值范围为_____________.
的取值范围为_____________.
【题目】“每天锻炼一小时,健康生活一辈子”,为了选拔“阳光大课堂”领操员校组织初中三个年级推选出来的15名领操员进行比赛,成绩如下表:
成绩/分 | 7 | 8 | 9 | 10 |
人数/人 | 2 | 5 | 4 | 4 |
若任意选择一名领操员的可能性相同
(1)任意选取一名领操员,选到成绩最低领操员的概率是_________.
(2)已知获得10分的选手中,七、八、九年级分别有1人,2人,1人,学校准备从中随机选取两人领操,求恰好选到八年级两名领操员的概率.