题目内容
【题目】数轴上O,A两点的距离为4,一动点P从点A出发,按以下规律跳动:第1次跳动到AO的中点A1处,第2次从A1点跳动到A1O的中点A2处,第3次从A2点跳动到A2O的中点A3处,按照这样的规律继续跳动到点A4,A5,A6,…,An.(n≥3,n是整数)处,那么线段AnA的长度为________(n≥3,n是整数).

【答案】4﹣![]()
【解析】
根据中点的性质,先算出第一次跳动后离远点的长度,同理继续算出第二次、第三次跳动后离原点的距离,然后观察每次距离的规律,用n表示出来![]() 的长度,最后用总长度减去
的长度,最后用总长度减去![]() 即可.
即可.
解:由于OA=4,
所有第一次跳动到OA的中点A1处时,OA1=![]() OA=
OA=![]() ×4=2,
×4=2,
同理第二次从A1点跳动到A2处,离原点的(![]() )2×4处,
)2×4处,
同理第二次从A2点跳动到A3处,离原点的(![]() )3×4处,
)3×4处,
同理跳动n次后,离原点的长度为(![]() )n×4=
)n×4=![]() ,
,
故线段AnA的长度为4﹣![]() (n≥3,n是整数).
(n≥3,n是整数).
故答案为:4﹣![]() .
.

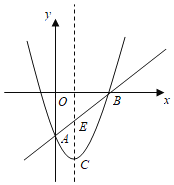
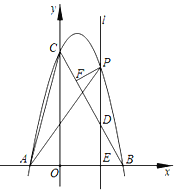
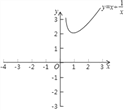
【题目】某数学兴趣小组对函数y=x+![]() 的图象和性质进行了探究,探究过程如下,请补充完整.
的图象和性质进行了探究,探究过程如下,请补充完整.
x | … | ﹣3 | ﹣2 | ﹣1 | - | - |
|
| 1 | 2 | 3 | … |
y | … | - | m | ﹣2 | - | - |
|
| 2 |
|
| … |
(1)自变量x的取值范围是 ,m= .
(2)根据(1)中表内的数据,在如图所示的平面直角坐标系中描点,画出函数图象的一部分,请你画出该函数图象的另一部分.
(3)请你根据函数图象,写出两条该函数的性质;
(4)进一步探究该函数的图象发现:
①方程x+![]() =3有 个实数根;
=3有 个实数根;
②若关于x的方程x+![]() =t有2个实数根,则t的取值范围是 .
=t有2个实数根,则t的取值范围是 .
【题目】由于雾霾天气频发,市场上防护口罩出现热销,某医药公司每月固定生产甲、乙两种型号的防雾霾口罩共20万只,且所有产品当月全部售出,原料成本、销售单价及工人生产提成如表:
| 甲 | 乙 |
原料成本 | 12 | 8 |
销售单价 | 18 | 12 |
生产提成 | 1 | 0.8 |
(1)若该公司五月份的销售收入为300万元,求甲、乙两种型号的产品分别是多少万只?
(2)公司实行计件工资制,即工人每生产一只口罩获得一定金额的提成,如果公司六月份投入总成本(原料总成本+生产提成总额)不超过239万元,应怎样安排甲、乙两种型号的产量,可使该月公司所获利润最大?并求出最大利润(利润=销售收入﹣投入总成本)
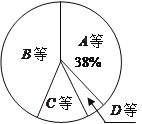
【题目】某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A、B、C、D四等,并绘制成下面的频数分布表和扇形统计图.
等第 | 成绩(得分) | 频数(人数) | 频率 |
A | 10分 | 7 | 0.14 |
9分 | x | m | |
B | 8分 | 15 | 0.30 |
7分 | 8 | 0.16 | |
C | 6分 | 4 | 0.08 |
5分 | y | n | |
D | 5分以下 | 3 | 0.06 |
合计 | 50 | 1.00 |
(1)试直接写出
(2)求表示得分为C等的扇形的圆心角的度数;
(3)如果该校九年级共有男生200名,试估计这200名男生中成绩达到A等和B等的人数共有多少人?