题目内容
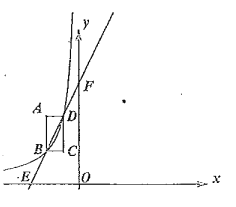
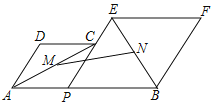
【题目】如图，已知AB=12，G、H是线段AB的三等分点，P为线段AB上的一个动点，分别以AP，PB为边在AB的同侧作菱形APCD和菱形PBFE，点P，C，E在一条直线上，
=
，M，N分别是对角线AC，BE的中点，在点P从点G运动到点H的过程中，MN的长度的取值范围是（）
A.
≤MN≤6B.≤MN≤
C.
≤MN≤6D.≤MN≤
【答案】B
【解析】
连接MP，NP，证明MP⊥NP，将M、N的距离转化为直角三角形的斜边，利用勾股定理结合二次函数图象，数形结合即可求解.
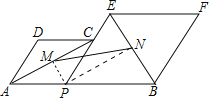
解：连接MP，NP，
∵G，H是线段AB的三等分点
∴AG=GH=HB=4
∵菱形APCD和菱形PBFE，∠DAP=60°，
∴MP=
AP，NP=
BP
∵M、N分别是对角线AC、BE的中点，
∴∠MPC=60°，∠EPN=30°，
∴MP⊥NP，
∴MN2=MP2+NP2，
即MN2=(AP)2+(BP)2
设PG=x，则PH=4-x，则AP=AG+PG=4+x，BP=BH+PH=4+4-x=8-x，其中0≤x≤4. 则MN2=
=
.，因为0≤x≤4，根据其二次函数的图象可知：当
时，MN2最大为52.当
时，MN2最小为28.故∴MN的长度的取值范围为
≤MN≤
.
故答案选：B
练习册系列答案
相关题目
【题目】根据学习函数的经验，探究函数y＝x2+ax﹣4|x+b|+4（b＜0）的图象和性质：
（1）下表给出了部分x，y的取值；
x | L | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | L |
y | L | 3 | 0 | ﹣1 | 0 | 3 | 0 | ﹣1 | 0 | 3 | L |
由上表可知，a＝ ，b＝ ；
（2）用你喜欢的方式在坐标系中画出函数y＝x2+ax﹣4|x+b|+4的图象；
（3）结合你所画的函数图象，写出该函数的一条性质；
（4）若方程x2+ax﹣4|x+b|+4＝x+m至少有3个不同的实数解，请直接写出m的取值范围．
