题目内容
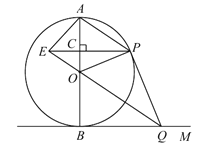
【题目】如图,△ABC内接于⊙O,BC是⊙O的直径,弦AF交BC于点E,∠CAF=2∠B.
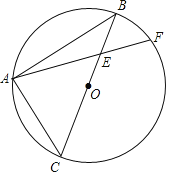
(1)求证:AE=AC;
(2)若⊙O的半径为4,E是OB的中点,求EF的长.
【答案】(1)见解析;(2)EF=![]()
【解析】
(1)过A作AH⊥CE于H,结合直径所对的圆周角是直角,得到∠ACB的余角∠CAH=∠ABC,结合∠CAF=2∠ABC,得到∠EAH=∠CAH,依据ASA证明△ACH≌△AEH,依据全等的性质即可;
(2)连接BF,先根据半径是4,及E是OB的中点,求出CE、BE;然后利用第(1)问∠CAH=∠ABC,及公共角∠C证明△CAH∽△CBA,依据相似的性质求得AC、AE,再依据同弧所对的圆周角相等,得到证明△CAE∽△FBE的条件,依据相似的性质即可求得EF的长.
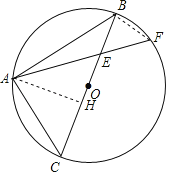
(1)证明:过A作AH⊥CE于H,
又∵BC是⊙O的直径,
∴∠CAB=∠AHC=∠AHE=90°,
∴∠ACB+∠ABC=∠ACB+∠CAH=90°,
∴∠CAH=∠ABC,
又∵∠CAF=2∠ABC,
∴∠EAH=∠CAH,
又∵AH=AH,
∴△ACH≌△AEH(ASA),
∴AC=AE;
(2)解:连接BF,
∵⊙O的半径为4,
∴BC=8,
∵E是OB的中点,
∴BE=OE=2,
∴CE=6,
∴CH=![]() CE=3,
CE=3,
∵∠CAH=∠ABC,∠C=∠C,
∴△CAH∽△CBA,
∴![]() ,
,
∴AC2=CHCB=3×8=24,
∴AE=AC=2![]() ,
,
∵∠F=∠C,∠FBE=∠CAE,
∴△CAE∽△FBE,
∴![]() ,
,
∴![]() ,
,
∴EF=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目