题目内容
【题目】如图，在平面直角坐标系xOy中，直线y=﹣3x+m与双曲线y= 
相交于点A（m，2）． 
（1）求双曲线y= 的表达式；
（2）过动点P（n，0）且垂直于x轴的直线与直线y=﹣3x+m及双曲线y= 的交点分别为B和C，当点B位于点C下方时，求出n的取值范围．
【答案】
（1）解：）∵点A（m，2）在直线y=﹣3x+m上，
∴2=﹣3m+m，
解得：m=﹣1，
∴A（﹣1，2）．
∵点A在双曲线 
上，
∴ 
，k=﹣2，
∴双曲线的表达式为y=﹣ 
．
（2）解：令y=﹣3x﹣1=﹣ ，
解得：x1=﹣1，x2= 
．
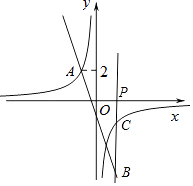
观察函数图象可知：当﹣1＜n＜0或n＞ 时，反比例函数图象在一次函数图象的上方，即点B位于点C下方，
∴当点B位于点C下方时，n的取值范围为﹣1＜n＜0或n＞ ．
【解析】（1）由点A的坐标利用一次函数图象上点的坐标特征即可求出m值，进而可得出点A的坐标，再由点A的坐标利用待定系数法即可求出双曲线的表达式；（2）令﹣3x﹣1=﹣ ，可求出两函数图象交点的横坐标，再根据两函数图象的上下位置关系即可得出当点B位于点C下方时，n的取值范围．
练习册系列答案
相关题目
【题目】八(2)班组织了一次经典诵读比赛，甲、乙两队各10人的比赛成绩如下表(10分制)：
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分，乙队成绩的众数是 分；
(2)计算乙队的平均成绩和方差；
(3)已知甲队成绩的方差是1.4，则成绩较为整齐的是 队．
