��Ŀ����
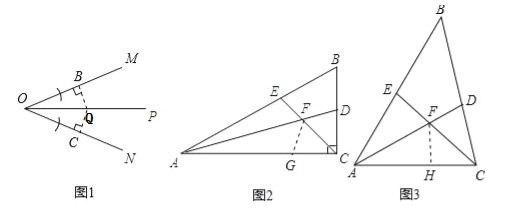
����Ŀ����ͼ1��OP����MON��ƽ���ߣ��������ø�ͼ�λ�һ����OP����ֱ��Ϊ�Գ����ȫ�������Σ��������ӵ�ȫ��������ע��ͼ�ϣ�
����ο������ȫ�������εķ���������������⣺
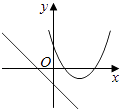
��1����ͼ2������ABC�У���ACB��ֱ�ǣ���B=60�㣬AD��CE�ֱ�����BAC����BCA��ƽ���ߣ�AD��CE�ཻ�ڵ�F������EFA�Ķ�����
��2���ڣ�1���������£����ж�FE��FD֮���������ϵ����˵�����ɣ�
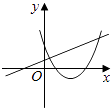
��3����ͼ3������ABC�У������ACB����ֱ�ǣ����� 1 ���е������������䣬�����ڣ�2�������ý����Ƿ���Ȼ����������������֤����������������˵�����ɣ�

���𰸡���1��60����2��FE=FD��3��FE=FD��Ȼ����
��������
��OM��ON�Ϸֱ��ȡOB��OC��ʹOB=OC���ֱ����B��C��OM��ON�Ĵ��ߣ������߽��ڵ�Q������OQ�����OBQ�ա�OCQ����1����֪��A CB=90�㣬��B=60�������������ε��ڽǺͶ����������BAC=30�㣮����AD��CE�ֱ�����BAC����BCA��ƽ���ߣ����ݽ�ƽ���ߵĶ��������DAC=15�㣬��ECA=45�㣮������������ǵ����ʼ��������EFA=60�㣻��2��FE=FD����AC�Ͻ�ȡAG=AE��֤����EAF�ա�GAF�� ����ȫ�������ε����ʿɵ�FE=FG����EFA=��GFA=60�㣮��֤����DFC=��GFC������ASA�ж���FDC�ա�FGC���ɴ˿ɵ�FD=FG���Ӷ�֤�� FE=FD����3����2���еĽ���FE=FD��Ȼ������֤����ȣ�2���ķ������.
��ͼ��ʾ����OBQ�ա�OCQ��
��1����ͼ2���ߡ�ACB=90�㣬��B=60�㣮
���BAC=30�㣮
��AD��CE�ֱ�����BAC����BCA��ƽ���ߣ�
���DAC=![]() ��BAC=15�㣬��ECA=
��BAC=15�㣬��ECA=![]() ��ACB=45�㣮
��ACB=45�㣮
���EFA=��DAC+��ECA=15��+45��=60�㣮
��2��FE=FD��
��ͼ2����AC�Ͻ�ȡAG=AE������FG��
��AD����BAC��ƽ���ߣ�
���EAF=��GAF��
����EAF����GAF��
��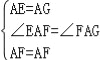
���EAF�ա�GAF��SAS����
��FE=FG����EFA=��GFA=60�㣮
���GFC=180�㩁60�㩁60��=60�㣮
���ߡ�DFC=��EFA=60�㣬
���DFC=��GFC��
����FDC����FGC��
��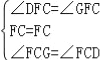
���FDC�ա�FGC��ASA����
��FD=FG��
��FE=FD��
��3����2���еĽ���FE=FD��Ȼ������
ͬ��2���ɵ���EAF�ա�HAF��
��FE=FH����EFA=��HFA��
���ɣ�1��֪��FAC=![]() ��BAC����FCA=
��BAC����FCA=![]() ��ACB��
��ACB��
���FAC+��FCA=![]() ����BAC+��ACB��=
����BAC+��ACB��=![]() =60�㣮
=60�㣮
���AFC=180�㩁����FAC+��FCA��=120�㣮
���EFA=��HFA=180�㩁120��=60�㣮
ͬ��2���ɵ���FDC�ա�FHC��
��FD=FH��
��FE=FD��

 �ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
�ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�