Question

【题目】如图，点E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，垂足分别为C、D．

（1）求证：ED=EC；

（2）求证：∠ECD=∠EDC；

（3）求证：OE垂直平分CD．

Answer 1

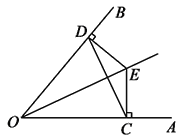
【答案】（1）见解析；（2）见解析；（3）见解析.

【解析】

（1）根据角平分线的性质进行判断；

（2）根据等边对等角即可得出结论；

（3）先判定Rt△OCE≌Rt△ODE（HL），得出OC=OD，进而得到点O在CD的垂直平分线上，再根据EC=DE，可得点E在CD的垂直平分线上，进而得到OE是CD的垂直平分线．

证明：（1）∵E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，

∴ED=EC；

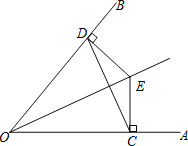
（2）∵EC=DE，

∴∠ECD=∠EDC；

（3）在Rt△OCE和Rt△ODE中，

，

∴Rt△OCE≌Rt△ODE（HL），

∴OC=OD，

∴点O在CD的垂直平分线上，

又∵EC=DE，

∴点E在CD的垂直平分线上，

∴OE垂直平分CD．