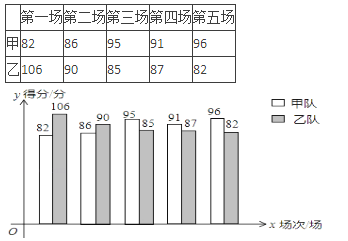
题目内容
【题目】先阅读下面例题的解法,然后解答问题:
例:若多项式2x3-x2+m分解因式的结果中有因式2x+1,求实数m的值.
解:设2x3-x2+m=(2x+1)·A(A为整式).
若2x3-x2+m=(2x+1)·A=0,则2x+1=0或A=0.
由2x+1=0,解得x=-![]() .
.
∴x=-![]() 是方程2x3-x2+m=0的解.
是方程2x3-x2+m=0的解.
∴2×(-![]() )3-(-
)3-(-![]() )2+m=0,即-
)2+m=0,即-![]() -
-![]() +m=0.
+m=0.
∴m=![]() .
.
请你模仿上面的方法尝试解决下面的问题:
若多项式x4+mx3+nx-16分解因式的结果中有因式(x-1)和(x-2),求实数m,n的值.
【答案】m=-5,n=20.
【解析】
参照题中方法设另一个整式是C,用解方程的思想求出x的值,代回原方程即可解题.
设x4+mx3+nx-16=(x-1)(x-2)·C(C为整式).
若x4+mx3+nx-16=(x-1)(x-2)·C=0,
则x-1=0或x-2=0或C=0,
由x-1=0或x-2=0,解得x=1或x=2.
∴x=1,x=2都是方程x4+mx3+nx-16=0的解.
∴14+m·13+n·1-16=0或24+m·23+n·2-16=0,
即m+n=15①,4m+n=0②,
①②联立解得m=-5,n=20.

练习册系列答案
相关题目