题目内容
【题目】如图,CD 和 BE 是△ABC 的两条高,∠BCD=45°,BF=FC,BE与 DF、DC分别交于点 G、H,∠ACD=∠CBE.
(1)证明:AB=BC;
(2)判断 BH 与 AE 之间的数量关系,并证明你的结论;
(3)结合已知条件,观察图形,你还能发现什么结论?请写出两个(不与前面结论相同).
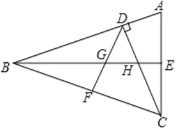
【答案】(1)见解析;(2)BH=2AE;(3)DF 平分∠BDC,DF⊥BC,DG=DH 等.
【解析】
(1)由CD和BE是ΔABC的两条高,于是得到∠A=∠ACD+∠A=90![]() ,于是得到∠ABE=∠ACD,因为∠ACD=∠CBE,折叠∠ABE=∠CBE,通过ΔBAE≌ΔBCE,根据全等三角形的性质得到BA=BC,于是得到结论;
,于是得到∠ABE=∠ACD,因为∠ACD=∠CBE,折叠∠ABE=∠CBE,通过ΔBAE≌ΔBCE,根据全等三角形的性质得到BA=BC,于是得到结论;
(2)根据等腰直角三角形的性质得到BD=DC证得ΔBDH≌ΔCDA,根据全等三角形的性质得到BH=AC,根据直角三角形的性质得到AC=2AE,BH=2AE,即可得到结论;
(3)根据等腰直角三角形的性质,即可得到DF平分∠BDC,DF⊥BC.根据等角的余角相等,即可得出DG=DH,
解: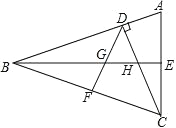
(1)∵CD 和 BE 是△ABC 的两条高,
∴∠ACD+∠A=90°=∠ABE+∠A,
∴∠ABE=∠ACD,
∵∠ACD=∠CBE,
∴∠ABE=∠CBE,
∵∠BEA=∠BEC=90°,
在△BAE 与△BCE 中,
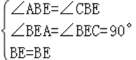
∴△BAE≌△BCE(AAS),
∴BA=BC;
(2)BH=2AE,理由:
∵∠BDC=90°,∠BCD=45°,
∴BD=DC,
∵∠BDH=∠CDA=90°, 在△BDH 与△CDA 中,
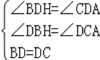
∴△BDH≌△CDA(AAS),
∴BH=AC,
∵BE⊥AC,
∴AC=2AE,
∴BH=2AE;
(3)存在:DF 平分∠BDC,DF⊥BC,DG=DH 等.理由:
∵△BCD 是等腰直角三角形,BF=CF,
∴DF 平分∠BDC,DF⊥BC;
∵∠ABE=∠CBE,∠BDH=∠BFG=90°,
∴∠BHD=∠BGF=∠DGH,
∴DG=DH.