题目内容
【题目】二次函数![]() 的图象经过点(﹣1,4),且与直线
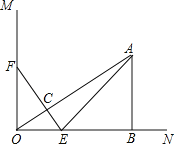
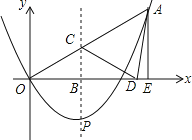
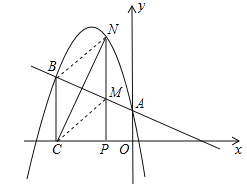
的图象经过点(﹣1,4),且与直线![]() 相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(﹣3,0).
相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(﹣3,0).
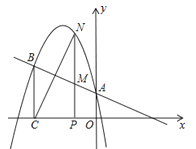
(1)求二次函数的表达式;
(2)点N是二次函数图象上一点(点N在AB上方),过N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;
(3)在(2)的条件下,点N在何位置时,BM与NC相互垂直平分?并求出所有满足条件的N点的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 时,MN和NC互相垂直平分.
时,MN和NC互相垂直平分.
【解析】
(1)先求得A、B的坐标,再利用待定系数法即可求得二次函数的解析式;
(2)设M的横坐标是x,则根据M和N所在函数的解析式,即可利用x表示出M、N的坐标,利用x表示出MN的长,利用二次函数的性质求解;
(3)BM与NC互相垂直平分,即四边形BCMN是菱形,则BC=MC,据此即可列方程,求得x的值,从而得到N的坐标.
(1)由题设可知A(0,1),B(﹣3,![]() ),根据题意得:
),根据题意得:
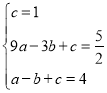 解得
解得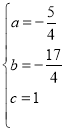 ,则二次函数的解析式是
,则二次函数的解析式是![]() ;
;
(2)设N(![]() ),则M、P的坐标分别为
),则M、P的坐标分别为![]() ,
,![]() ,∴MN=PN-PM=
,∴MN=PN-PM=![]() ,则当
,则当![]() 时,MN的最大值为
时,MN的最大值为![]() ;
;
(3)连接MC、BN、BM与NC互相垂直平分,即四边形BCMN是菱形,由于BC∥MN,即MN=BC,且BC=MC,即![]() ,且
,且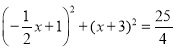 ,解得
,解得![]() ,故当
,故当![]() 时,MN和NC互相垂直平分.
时,MN和NC互相垂直平分.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目