题目内容
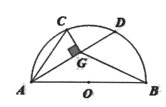
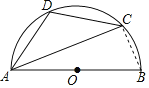
【题目】如图,AB是半圆的直径,C、D是半圆上的两点,且∠BAC=16°,![]() =
=![]() .求四边形ABCD各内角的度数.
.求四边形ABCD各内角的度数.
【答案】四边形ABCD各内角的度数为53°,74°,127°,106°.
【解析】
根据AB是直径可得∠ACB=90°,由∠BAC=16°,可得∠B=74°,根据圆内接四边形对角互补可知∠D=106°,根据![]() =
=![]() ,可得∠DAC=∠DCA=37°,然后易得答案.
,可得∠DAC=∠DCA=37°,然后易得答案.
解:如图,
∵AB是半圆的直径,
∴∠ACB=90°,
∵∠BAC=16°,
∴∠B=74°,
∵四边形ABCD是圆O的内接四边形,
∴∠D=180°﹣∠B=106°,
∵![]() =
=![]() ,
,
∴∠DAC=∠DCA=![]() (180°﹣106°)=37°,
(180°﹣106°)=37°,
∴∠DAB=∠DAC+∠BAC=53°,∠DCB=∠DCA+∠ACB=127°,
即四边形ABCD各内角的度数为53°,74°,127°,106°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目