Question

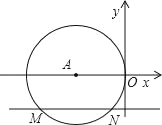
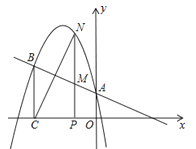
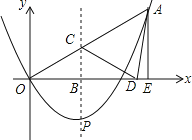
【题目】如图，在平面直角坐标系中，已知抛物线的对称轴为，且经过点A（2，1），点是抛物线上的动点，的横坐标为，过点作轴，垂足为，交于点，点关于直线的对称点为，连接，，过点A作AE⊥x轴，垂足为E．则当（ ）时，的周长最小.

A.1B.1.5C.2D.2.5

Answer 1

【答案】A

【解析】

因为O与D关于直线PB的对称，所以PB垂直平分OD，则CO=CD，因为，△ACD的周长=AC+CD+AD=AC+CO+AD=AO+AD，AO=，所以当AD最小时，△ACD的周长最小；根据垂线段最短，可知此时点D与E重合，其横坐标为2，故m=1．

∵O与D关于直线PB的对称，

∴PB垂直平分OD，

∴CO=CD，

∵△ACD的周长=AC+CD+AD=AC+CO+AD=AO+AD，AO=，

∴当AD最小时，△ACD的周长最小；

∴此时点D与E重合，其横坐标为2，故m=1．
故选A.