题目内容
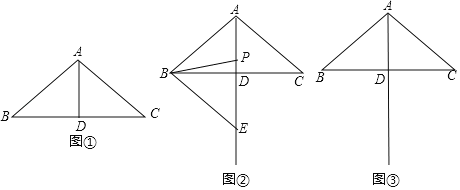
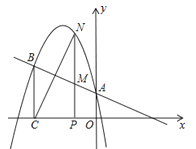
【题目】如图,已知∠MON=90°,A是∠MON内部的一点,过点A作AB⊥ON,垂足为点B,AB=3厘米,OB=4厘米,动点E、F同时从O点出发,点E以1.5厘米/秒的速度沿ON方向运动,点F以2厘米/秒的速度沿OM方向运动,EF与OA交于点C,连接AE,当点E到达点B时,点F随之停止运动,设运动时间为t秒(t>0).
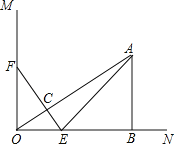
(1)当t=1秒时,△EOF与△ABO是否相似?请说明理由;
(2)在运动过程中,不论t取何值,总有EF⊥OA,为什么?
(3)在运动过程中,是否存在某一时刻t,使得△AEB与△OEF相似?
【答案】(1)△EOF∽△ABO.理由见解析;(2)见解析;(3)当t=![]() 时,存在△OEF∽△BEA.
时,存在△OEF∽△BEA.
【解析】
(1)运用两边对应成比例且夹角相等,即可得出△EOF∽△ABO;
(2)证明Rt△EOF∽Rt△ABO,得出对应角相等,即可得到∠FCO=90°,进而可得EF⊥OA;
(3)分两种情况讨论:△OEF∽△BEA;△OEF∽△BAE,分别依据对应边成比例,求得t的值,再根据题意判断是否符合题意即可.
(1)△EOF∽△ABO;
理由:∵t=1,
∴OE=1.5厘米,OF=2厘米,
∵AB=3厘米,OB=4厘米,
∴![]() =
=![]() ,
,![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵∠EOF=∠ABE=90°,
∴△EOF∽△ABO;
(2)在运动过程中,OE=1.5t,OF=2t.
∵AB=3,OB=4,
∴![]() =
=![]() ,
,![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
又∵∠EOF=∠ABO=90°,
∴Rt△EOF∽Rt△ABO,
∴∠AOB=∠EFO.
∵∠AOB+∠FOC=90°,
∴∠EFO+∠FOC=90°,即∠FCO=90°,
∴EF⊥OA;
(3)由题可得∠EOF=∠ABE=90°,
若△OEF∽△BEA,则![]() ,
,
∴![]() ,
,
解得t=![]() (符合题意);
(符合题意);
若△OEF∽△BAE,则![]() ,
,
∴![]() ,
,
解得t=0(不合题意),
综上所述,当t=![]() 时,存在△OEF∽△BEA.
时,存在△OEF∽△BEA.

【题目】小华是数学兴趣小组的一名成员,他在学过二次函数的图像与性质之后,对![]() 的图像与性质进行了探究,探究过程如下,请你补充完整.
的图像与性质进行了探究,探究过程如下,请你补充完整.
(1)小刚通过计算得到几组对应的数值如下
| … |
|
|
|
|
|
| 0 | 1 |
| 2 | 3 | 4 | 5 | … |
| … |
| 0 | 4 | 6 |
| 6 | 4 | 6 |
| 6 | 4 | 0 |
| … |
填空:自变量的取值范围是__________________,![]() __________.
__________.
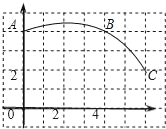
(2)在如图所示的平面直角坐标系中,描出上表中各组对应数值的点,并根据描出的点,画出该函数的图像.
(3)请你根据画出的图像,写出此函数的两条性质;
①__________________________________________;
②__________________________________________.
(4)直线![]() 经过
经过![]() ,若关于
,若关于![]() 的方程
的方程![]() 有4个不相等的实数根,则
有4个不相等的实数根,则![]() 的取值范围为_________.
的取值范围为_________.

【题目】表中所列 ![]() 的7对值是二次函数
的7对值是二次函数![]() 图象上的点所对应的坐标,其中
图象上的点所对应的坐标,其中 ![]()
x | … |
|
|
|
|
|
|
| … |
y | … | 7 | m | 14 | k | 14 | m | 7 | … |
根据表中提供的信息,有以下4 个判断:
① ![]() ;②
;② ![]() ;③ 当
;③ 当![]() 时,y 的值是 k;④
时,y 的值是 k;④ ![]() 其中判断正确的是 ( )
其中判断正确的是 ( )
A. ①②③ B. ①②④ C. ①③④ D. ②③④