题目内容
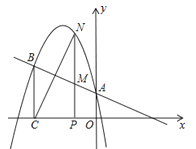
【题目】如图,在平面直角坐标系中,已知点![]() ,以原点O为圆心、3为半径作⊙O,⊙O与x轴交于点B、C.点P从点O出发,以每秒1个单位的速度沿y轴正半轴运动,运动时间为
,以原点O为圆心、3为半径作⊙O,⊙O与x轴交于点B、C.点P从点O出发,以每秒1个单位的速度沿y轴正半轴运动,运动时间为![]() .连结AP,将
.连结AP,将![]() 沿AP翻折,得到
沿AP翻折,得到![]() ,求
,求![]() 有一边所在直线与⊙O相切时
有一边所在直线与⊙O相切时![]() 的值.
的值.

【答案】![]() 或
或![]() 或
或![]() .
.
【解析】
分三种情况,先求得OQ,进而根据三角形面积公式求得AP,然后根据勾股定理列出方程,解方程即可.
解:当AQ与⊙O相切时,如图1,

设AQ切⊙O于点D,连接OQ,交AP于M,连接OD,
∵AD切⊙O于点D,
∴OD⊥AQ,OD=3,
∵OA=5,
∴AD=4,
∵A(5,0),
OA=AQ=5,
∴QD=1,
∴OQ=![]()
∵将△OAP沿AP翻折,得到△APQ.
∴OQ⊥AP,OM=MQ=![]()
∵OP=t,OA=5,
∴![]() APOM=
APOM=![]() OAOP,即
OAOP,即![]() AP
AP![]() =
=![]() 5t,
5t,
∴AP=![]() t,
t,
在Rt△AOP中,AP2=OP2+OA2,解10t2=t2+25,
解得t=![]() ;
;
当AP与⊙O相切时,如图2,
,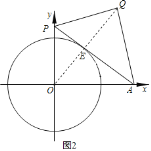
设AP切⊙O于点E,连接OQ,
∵将△OAP沿AP翻折,得到△APQ.
∴OQ⊥AP,
∴OQ经过点E,
∴OE⊥AP,
∵![]() APOE=
APOE=![]() OAOP,即3AP=5t,
OAOP,即3AP=5t,
∴AP=![]() t,
t,
在Rt△AOP中,AP2=OP2+OA2,解(![]() t)2=t2+25,
t)2=t2+25,
解得t=![]() ,
,
当PQ与⊙O相切时,如图3,

设PQ切⊙O于点E,连接OE,
∴OE⊥PQ,
∵AQ⊥PQ,
∴OE∥AQ,
∴△ODE∽△ADQ,
![]() 即
即![]()
∴PD=DQ-PQ=![]() -t,
-t,
∵![]() ODOP=
ODOP=![]() PDOE,
PDOE,

解得t=![]()
综上,△APQ有一边所在直线与⊙O相切时t的值为![]() 或
或![]() 或
或![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目