题目内容
【题目】如图,抛物线y=x2![]() 2x+c的顶点A在直线l:y=x
2x+c的顶点A在直线l:y=x![]() 5上.
5上.
(1)求抛物线顶点A的坐标;
(2)设抛物线与y轴交于点B,与x轴交于点C、D(C点在D点的左侧),试判断△ABD的形状;
(3)在直线l上是否存在一点P,使以点P、A、B、D为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.

【答案】(1)A(1,﹣4);
(2)△ABD是直角三角形,理由见解析;
(3)存在点P(﹣2,﹣7)或P(4,﹣1),使以点A、B、D、P为顶点的四边形是平行四边形.
【解析】试题分析:(1)先根据抛物线的解析式得出其对称轴方程,由此得到顶点A的横坐标,然后代入直线l的解析式中即可求出点A的坐标.
(2)由A点坐标可确定抛物线的解析式,进而可得到点B的坐标.则AB、AD、BD三边的长可得,然后根据边长确定三角形的形状.
(3)若以点P、A、B、D为顶点的四边形是平行四边形,应分①AB为对角线、②AD为对角线两种情况讨论,然后结合勾股定理以及边长的等量关系列方程求出P点的坐标.
(1)∵顶点A的横坐标为![]() ,且顶点在y=x﹣5上,
,且顶点在y=x﹣5上,
∴当x=1时,y=1-5=-4,
∴A(1,-4).
(2)将A(1,-4)代入y=x2-2x+c,可得,1-2+c=-4,c=-3,
∴y=x2-2x-3,
∴B(0,-3)
当y=0时,x2-2x-3=0,x1=-1,x2=3
∴C(-1,0),D(3,0),
∵BD2=OB2+OD2=18,AB2=(4-3)2+12=2,AD2=(3-1)2+42=20,
∴BD2+AB2=AD2,
∴∠ABD=90°,即△ABD是直角三角形.
(3)由题意知:直线y=x-5交y轴于点E(0,-5),交x轴于点F(5,0)
∴OE=OF=5,
又∵OB=OD=3
∴△OEF与△OBD都是等腰直角三角形
∴BD∥l,即PA∥BD
则构成平行四边形只能是PADB或PABD,如图,
过点P作y轴的垂线,过点A作x轴的垂线交过P且平行于x轴的直线于点G.
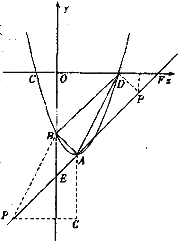
设P(x1,x1-5),则G(1,x1-5)
则PG=|1-x1|,AG=|5-x1-4|=|1-x1|
PA=BD=3![]()
由勾股定理得:
(1-x1)2+(1-x1)2=18,x12-2x1-8=0,x1=-2或4
∴P(-2,-7)或P(4,-1),
存在点P(-2,-7)或P(4,-1)使以点A、B、D、P为顶点的四边形是平行四边形.