题目内容
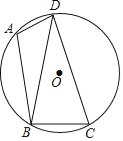
【题目】如图，已知四边形ABCD内接于圆O，连结BD，∠BAD=100°，∠DBC=80°．
（1）求证：BD=CD；
（2）若圆O的半径为9，求
的长（结果保留π）．
【答案】(1)见解析(2) 2π
【解析】分析：（1）直接利用圆内接四边形的对角互补得出∠DCB的度数，再利用∠DCB=∠DBC求出答案；
（2）首先求出
的度数，再利用弧长公式直接求出答案．
详解：（1）∵四边形ABCD内接于圆O，∴∠DCB+∠BAD=180°．
∵∠BAD=100°，∴∠DCB=180°﹣100°=80°．
∵∠DBC=80°，∴∠DCB=∠DBC=80°，∴BD=CD；
（2）∵∠DCB=∠DBC=80°，∴∠BDC=20°，由圆周角定理，得：的度数为：40°，故的长=
=2π．
答：的长为2π．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
