题目内容
【题目】如图，在平面直角坐标系中，已知点A（0，1）、点B（0，1+t）、C（0，1﹣t）（t＞0），点P在以D（3，5）为圆心，1为半径的圆上运动，且始终满足∠BPC=90°，则t的最小值是（ ）
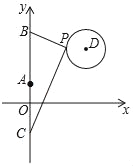
A. 3 B. 4 C. 5 D. 6
【答案】B
【解析】分析：先求出AB，AC，进而得出AC=AB，结合直角三角形的斜边的中线等于斜边的一半，即AP=t，即可得出t最小时，点P在AD上，用两点间的距离公式即可得出结论．
详解：如图，连接AP．
∵点A（0，1）、点B（0，1+t）、C（0，1﹣t）（t＞0），∴AB=（1+t）﹣1=t，AC=1﹣（1﹣t）=t，∴AB=AC．
∵∠BPC=90°，∴AP=
BC=AB=t，要t最小，就是点A到⊙D上的一点的距离最小，∴点P在AD上．
∵A（0，1），D（3，5），∴AD=
=5，∴t的最小值是AP=AD﹣PD=5﹣1=4．
故选B．
练习册系列答案
相关题目
