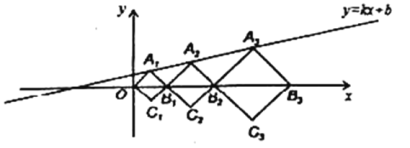
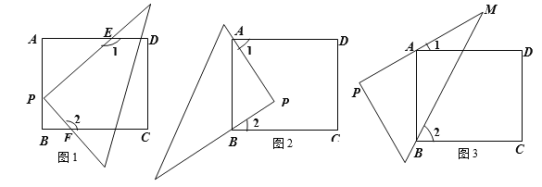
��Ŀ����
����Ŀ��Ϊ�ⷽ�̣�x2��1��2��5��x2��1��+4=0�����ǿ��Խ�x2��1��Ϊһ�����壬Ȼ����x2��1=y����
��x2��1��=y2��ԭ���̻�Ϊy2��5y+4=0����
���y1=1��y2=4
��y=1ʱ��x2��1=1����x2=2����x=��![]() ��
��
��y=4ʱ��x2��1=4����x2=5����x=��![]() ��
��
��ԭ���̵Ľ�Ϊx1=![]() ��x2=��
��x2=��![]() ��x3=
��x3=![]() ��x4=��
��x4=��![]()
������⣺
��1����գ�����ԭ���̵õ����̢ٵĹ����У������� �����ﵽ�˽��ε�Ŀ�ģ��������� ������ѧ˼�룮
��2���ⷽ�̣�x4��x2��6=0��
���𰸡���1����Ԫ��ת������2��x=��![]() ��
��
�������������������1������ԭ���̵õ����̢ٵĹ����У����û�Ԫ���ﵽ�˽��ε�Ŀ�ģ�������ת������ѧ˼�룻
��2����![]() ��ԭ���̿ɻ�Ϊ����
��ԭ���̿ɻ�Ϊ����![]() �ķ��̣�������̵Ľ�õ�
�ķ��̣�������̵Ľ�õ�![]() ��ֵ������ȷ����
��ֵ������ȷ����![]() ��ֵ��
��ֵ��
�����������1������ԭ���̵õ����̢ٵĹ����У����û�Ԫ���ﵽ�˽��ε�Ŀ�ģ�������ת������ѧ˼�룻
�ʴ�Ϊ����Ԫ��ת����
��2����![]() ��ԭ���̿ɻ�Ϊ
��ԭ���̿ɻ�Ϊ![]()
��ã� ![]()
![]()
![]() ��
��![]()
��![]()

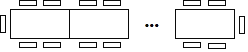
����Ŀ��Ϊ����ף���70�����գ�������ѧ�����������70������������ϵ�л��ѧУ��ίΪ����֯�ô�������ٱ��ݣ������鲿�����꼶ѧ�������ߣ���ѧ�����߷ֳ��ĸ��飬�����Ƴ����²�������ͳ��ͼ����
��� | ���� | ���� |
1�� |
| 15 |
2�� |
|
|
3�� |
|
|
4�� |
| 10 |
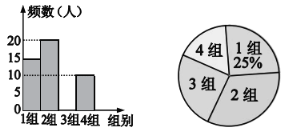
����������Ϣ������������⣺
��1����ͳ�Ʊ��У�![]() ��ֵ��________�����ε����ѧ��������________��.
��ֵ��________�����ε����ѧ��������________��.
��2����ȫƵ���ֲ�ֱ��ͼ.
��3��������������������У��ж��γ������������ѧ��������Ӧ����![]() �ķ�Χ����У���꼶480��ѧ���У����߷��ϸ�������ѧ��Լ�ж����ˣ�
�ķ�Χ����У���꼶480��ѧ���У����߷��ϸ�������ѧ��Լ�ж����ˣ�
����Ŀ��ij���г���һ���ڼƻ�ƽ��ÿ������200�����г�����������ԭ��ʵ��ÿ����������ƻ�������г��룮�±���ij�ܵ����������������Ϊ����������Ϊ������
���� | һ | �� | �� | �� | �� | �� | �� |
��������/�� |
|
|
|
|
|
|
|
��1�����ݼ�¼�����ݿ�֪���ó��������������г� ����
��2�������ϱ���¼�����ݿ�֪���ó�����ʵ���������г� ����
��3���ó�ʵ��ÿ�ռƼ������ƣ�ÿ����һ�����г��ɵ�60Ԫ���������������������ÿ�����⽱��15Ԫ�����겻��ÿ��ļƻ�������������һ����20Ԫ����ô�ó�������һ�ܵĹ����ܶ��Ƕ���Ԫ��
��4�����ó�ʵ��ÿ�ܼƼ������ƣ�ÿ����һ�����г��ɵ�60Ԫ������������ܼƻ���������������ÿ�����⽱��15Ԫ�����겻��ÿ�ܵļƻ�������������һ����20Ԫ����ô�ó�������һ�ܵĹ����ܶ��Ƕ���Ԫ��