题目内容
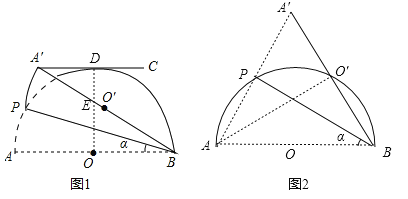
【题目】图1和图2,半圆O的直径AB=4,点P(不与点A,B重合)为半圆上一点,将图形沿着BP折叠,分别得到点A,O的对称点A′,O′,设∠ABP=α.
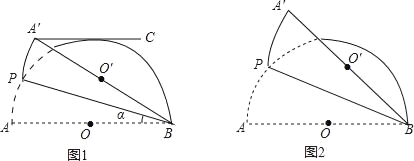
(1)如图1,当α=22.5°时,过点A′作A′C∥AB,判断A′C与半圆O的位置关系,并说明理由.
(2)如图2,当α= 时,点O′落在![]() 上.当α= 时,BA′与半圆O相切.
上.当α= 时,BA′与半圆O相切.
(3)当线段B O′与半圆O只有一个公共点B时,α的取值范围是 .
【答案】(1)相离(2) 30°;45° (3) 0°<α<30°或45°≤α<90°
【解析】分析:(1)过O作OD⊥A′C于点D,交A′B于点E,利用含30°角的直角三角形的性质可求得DE+OE=![]() A′B=
A′B=![]() AB>OA,可判定A′C与半圆相离;
AB>OA,可判定A′C与半圆相离;
(2)当O′在![]() 上时,连接AO′,则可知BO′=
上时,连接AO′,则可知BO′=![]() AB,可求得∠O′BA=60°,可求得α=30°,当BA′与半圆相切时,可知OB⊥A′B,则可知α=45°;
AB,可求得∠O′BA=60°,可求得α=30°,当BA′与半圆相切时,可知OB⊥A′B,则可知α=45°;
(3)利用(2)可知当α=30°时,线段O′B与圆交于O′,当α=45°时交于点B,结合题意可得出满足条件的α的范围.
详解:(1)相离,理由如下:
如图1,过O作OD过O作OD⊥A′C于点D,交A′B于点E,
∵α=22.5°,A′C∥AB,∴∠ABA′=∠CA′B=45°,∴DE=![]() A′E,OE=
A′E,OE=![]() BE,∴DO=DE+OE=
BE,∴DO=DE+OE=![]() (A′E+BE)=
(A′E+BE)=![]() AB>OA,∴A′C与半圆O相离;
AB>OA,∴A′C与半圆O相离;
(2)当O′在![]() 上时,如图2,
上时,如图2,
连接AO′,则可知BO′=![]() AB,∴∠O′AB=30°,∴∠ABO′=60°,∴α=30°;
AB,∴∠O′AB=30°,∴∠ABO′=60°,∴α=30°;
当BA′与半圆O相切时,则OB⊥BA′,∴∠OBA′=2α=90°,∴α=45°.
故答案为:30°;45°;
(3)∵点P,A不重合,∴α>0,由(2)可知当α增大到30°时,点O′在半圆上,∴当0°<α<30°时点O′在半圆内,线段BO′与半圆只有一个公共点B;
当α增大到45°时BA′与半圆相切,即线段BO′与半圆只有一个公共点B.
当α继续增大时,
综上所述:0°<α<30°或45°≤α<90°.
故答案为:0°<α<30°或45°≤α<90°.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案【题目】某自行车厂一周内计划平均每天生产200辆自行车,由于种种原因,实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产记为正,减产记为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减产量/辆 |
|
|
|
|
|
|
|
(1)根据记录的数据可知,该厂星期五生产自行车 辆.
(2)根据上表记录的数据可知,该厂本周实际生产自行车 辆.
(3)该厂实行每日计件工资制,每生产一辆自行车可得60元,若超额完成任务,则超过部分每辆另外奖励15元,若完不成每天的计划量,则少生产一辆扣20元,那么该厂工人这一周的工资总额是多少元?
(4)若该厂实行每周计件工资制,每生产一辆自行车可得60元,若超额完成周计划工作量,则超过部分每辆另外奖励15元,若完不成每周的计划量,则少生产一辆扣20元,那么该厂工人这一周的工资总额是多少元?