题目内容
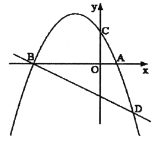
【题目】如图,抛物线![]() 与x轴交于点
与x轴交于点![]() ,点
,点![]() ,与y轴交于点C,且过点
,与y轴交于点C,且过点![]() .点P、Q是抛物线
.点P、Q是抛物线![]() 上的动点.
上的动点.
(1)求抛物线的解析式;
(2)当点P在直线OD下方时,求![]() 面积的最大值.
面积的最大值.
(3)直线OQ与线段BC相交于点E,当![]() 与
与![]() 相似时,求点Q的坐标.
相似时,求点Q的坐标.

【答案】(1)抛物线的表达式为:![]() ;(2)
;(2)![]() 有最大值,当
有最大值,当![]() 时,其最大值为
时,其最大值为![]() ;(3)
;(3) ![]() 或
或![]() 或
或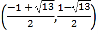 或
或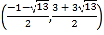 .
.
【解析】
(1)函数的表达式为:y=a(x+1)(x-3),将点D坐标代入上式,即可求解;
(2)设点![]() ,求出
,求出![]() ,根据
,根据![]()
![]()
![]() ,利用二次函数的性质即可求解;
,利用二次函数的性质即可求解;
(3)分∠ACB=∠BOQ、∠BAC=∠BOQ,两种情况分别求解,通过角的关系,确定直线OQ倾斜角,进而求解.
解:(1)函数的表达式为:![]() ,将点D坐标代入上式并解得:
,将点D坐标代入上式并解得:![]() ,
,
故抛物线的表达式为:![]() …①;
…①;
(2)设直线PD与y轴交于点G,设点![]() ,
,
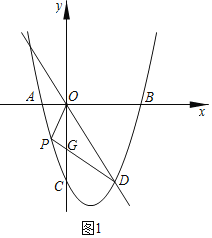
将点P、D的坐标代入一次函数表达式:![]() 并解得,直线PD的表达式为:
并解得,直线PD的表达式为:![]() ,则
,则![]() ,
,
![]()
![]()
![]() ,
,
∵![]() ,故
,故![]() 有最大值,当
有最大值,当![]() 时,其最大值为
时,其最大值为![]() ;
;
(3)∵![]() ,∴
,∴![]() ,
,
∵![]() ,故
,故![]() 与
与![]() 相似时,分为两种情况:
相似时,分为两种情况:
①当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
过点A作AH⊥BC与点H,
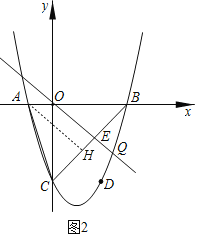
![]() ,解得:
,解得:![]() ,
,
∴CH=![]()
则![]() ,
,
则直线OQ的表达式为:![]() …②,
…②,
联立①②并解得:![]() ,
,
故点![]() 或
或![]() ;
;
②![]() 时,
时,
![]() ,
,
则直线OQ的表达式为:![]() …③,
…③,
联立①③并解得:![]() ,
,
故点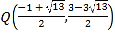 或
或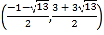 ;
;
综上,点![]() 或
或![]() 或
或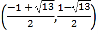 或
或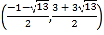 .
.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目