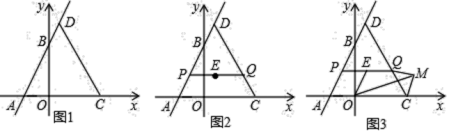Question

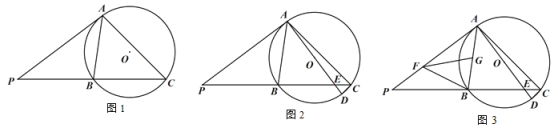
【题目】已知：△ABC 内接于⊙O，过点 A 作⊙O 的切线交 CB 的延长线于点 P，且∠PAB=45°．

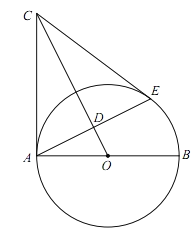
（1）如图 1，求∠ACB 的度数；

（2）如图 2，AD 是⊙O 的直径，AD 交 BC 于点 E，连接 CD，求证：AC CD ；

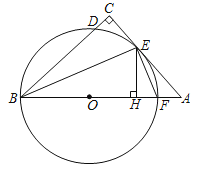
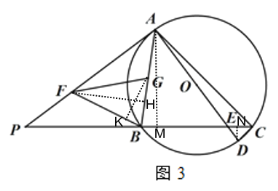
（3）如图 3 ，在（2）的条件下，当 BC 4CD 时，点 F，G 分别在 AP，AB 上，连接 BF，FG，∠BFG=∠P，且 BF=FG，若 AE=15，求 FG 的长．

Answer 1

【答案】（1）∠ACB＝45°；（2）见解析；（3）

【解析】

（1）连接OA，OB，根据切线的性质求出∠OAB＝∠OBA＝45°，得到∠AOB＝90°，再根据圆周角定理可得答案；

（2）作AM⊥BC于M，DN⊥BC于N，连接BD，易求，，然后证明△ABM≌△BDN，得到AM＝BN，等量代换即可得证；

（3）根据（2）中结论求出，然后证明△AMC∽△DNC，AM∥DN，根据相似三角形的性质和平行线分线段成比例定理求得DE和AD，进而利用勾股定理求出CD，AC，然后即可求出AB的长，再证明△PAB∽△PCA，求出PA，可得，过点G作GK⊥FB，过点F作FH⊥BG，设GK＝3b，利用三角函数及等腰三角形的性质求出AH和BH，然后列方程求出b值即可解决问题．

解：（1）连接OA，OB，则OA＝OB，

∴∠OAB＝∠OBA，

∵PA是⊙O的切线，

∴∠PAO＝90°，

∵∠PAB＝45°，

∴∠OAB＝∠OBA＝45°，

∴∠AOB＝90°，

∴∠ACB＝∠AOB＝45°；

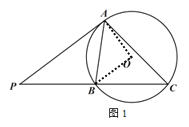
（2）作AM⊥BC于M，DN⊥BC于N，连接BD，

∵AD是⊙O的直径，

∴∠ABD＝∠ACD＝90°，

∵∠ACB＝45°，

∴∠CAM＝∠BCD＝∠CDN＝45°，

∴，，

∵∠ADB＝∠ACB＝45°，

∴AB＝BD，

∵∠ABM＋∠DBN＝90°＝∠BDN＋∠DBN，

∴∠ABM＝∠BDN，

又∵∠AMB＝∠BND＝90°，

∴△ABM≌△BDN（AAS），

∴AM＝BN，

∴；

（3）如图3，作AM⊥BC于M，DN⊥BC于N，由（2）可知：，

∵，

∴，即，

设CD＝x，则AC＝7x，

∵∠AMC＝∠DNC＝90°，∠ACM＝∠DCN＝45°，

∴△AMC∽△DNC，

∴，

∵AM⊥BC，DN⊥BC，

∴AM∥DN，

∴，

∴，

∴，，

在Rt△ACD中，AC2+CD2＝AD2，

∴，

解得：（负值已舍去），

∴，，，

∵△AMC是等腰直角三角形，

∴，

∴，

∴，

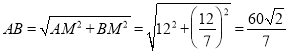∵∠P＝∠P，∠PAB＝∠PCA＝45°，

∴△PAB∽△PCA，

∴，

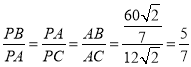设PB＝5a，则PA＝7a，

由PA2＝PB·PC得：，

解得：或a＝0（舍去），

∴PA＝20，

∴，

∴，

过点G作GK⊥FB，过点F作FH⊥BG，

设GK＝3b，则BF＝FG＝5b，

∴FK＝4b，

∴BK＝b，

∴，

∴BH，

∴，

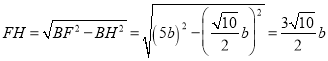∵∠PAB＝45°，

∴AH＝FH＝，

∴，

解得：，

∴．