题目内容
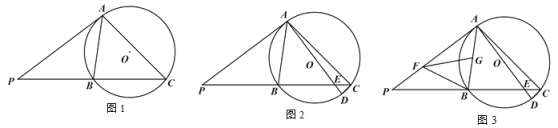
【题目】如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
(1)求证:AC是⊙O的切线;
(2)过点E作EH⊥AB,垂足为H,若CD=1,EH=3,求BE长.

【答案】(1)详见解析;(2)![]()
【解析】
(1)连结OE,根据BE平分∠ABC,可得∠CBE=∠ABE,证明OE∥BC,进而可以证明AC是⊙O的切线;
(2)连结DE,根据BE平分∠ABC,AC⊥BC,EH⊥AB,可得CE=EH,再证明Rt△CDE≌△Rt△HFE,得CD=HF,利用勾股定理求出OE,再利用勾股定理即可求得BE的长.
解:(1)连结OE,
∵BE平分∠ABC,
∴∠CBE=∠ABE,
又∵OB=OE,
∴∠ABE=∠BEO,
∴∠CBE=∠BEO,
∴OE∥BC,
∵∠C=90°,即AC⊥BC,
∴OE⊥AC,
∴AC是⊙O的切线;
(2)连结DE,
∵BE平分∠ABC,AC⊥BC,EH⊥AB,

∴CE=EH,DE=EF,
∴Rt△CDE≌△Rt△HFE(HL),
∴CD=HF,
∵CD=1,
∴HF=1,
∵OE2=OH2+HE2,
∴OE2=(OE﹣1)2+32,
∴OE=5,
∴BH=9,
∴![]() .
.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目