Question

【题目】矩形OABC在平面直角坐标系中的位置如图所示，O为坐标原点，点B的坐标为(10，8)，连接AC，已知反比例函数y=(m≠0)在第一象限的图象经过矩形OABC的对角线的交点D，并交BC于点E，交AB于点F．

（1）求线段AC所在直线的解析式和m的值．

（2）连接OE，OF，EF，求△OEF的面积．

Answer 1

【答案】（1）y=x+8，20；（2）

【解析】

（1）先利用B点的坐标及矩形的性质求出A，C的坐标，然后利用待定系数法即可求出线段AC所在直线的解析式，再利用A，C的坐标求出点D的坐标，然后代入反比例函数解析式中即可求出m的值；

（2）先利用反比例函数的解析式求出E，F的坐标，然后利用即可求解．

解：(1)∵四边形ABCD是矩形，

∴．

∵点B的坐标为 ，

∴，

∴．

设线段AC所在的直线的解析式为

将代入解析式中得

解得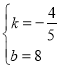

∴线段AC所在的直线的解析式为．

∵点D为对角线AC的中点，

∴点D的坐标为，

∵反比例函数 (m≠0)在第一象限的图象经过矩形OABC对角线的交点D，

∴ ；

(2) 当时， ，当时，有 ，解得．

∵比例函数的图象交BC于点E，交AB于点F，

∴点E的坐标为，点F的坐标为，

∴BE= ，BF= ，

．