题目内容
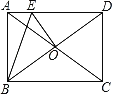
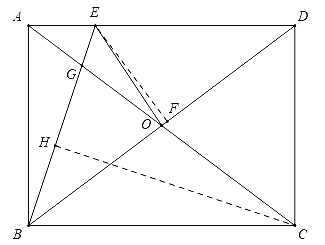
【题目】如图,矩形ABCD的对角线AC与BD交于点O,点E在AD上,且DE=CD,连接OE,∠ABE=![]() ∠ACB,若AE=2,则OE的长为_____.
∠ACB,若AE=2,则OE的长为_____.
【答案】![]()
【解析】
注意到∠ABE=![]() ACB,于是作CH⊥BE于H,EF⊥BD于F.设BE与AC的交点为G.推出△CBG与△AGE均为等腰三角形,设矩形的宽为x,然后表示出BC和AC的长度,由勾股定理列方程解出x,接下来利用∠ADB的正弦值和余弦值求出EF和OF,EF的长度,OE的长度也就可以算出来了.
ACB,于是作CH⊥BE于H,EF⊥BD于F.设BE与AC的交点为G.推出△CBG与△AGE均为等腰三角形,设矩形的宽为x,然后表示出BC和AC的长度,由勾股定理列方程解出x,接下来利用∠ADB的正弦值和余弦值求出EF和OF,EF的长度,OE的长度也就可以算出来了.
解:如图,作CH⊥BE于H,EF⊥BD于F.设BE与AC的交点为G.
则∠HBC+∠BCH=∠BHC=90°,
∵四边形ABCD为矩形,
∴AD=BC,AB=CD,∠ABC=∠BAD=90°,AD∥BC,AC=BD
∴∠ABE+∠CBH=90°,
∴∠ABE=∠BCH,
∵∠ABE=![]() ∠ACB,
∠ACB,
∴∠BCH=∠GCH,
∴BH=GH,BC=CG,∠CBH=∠CGH,
设AB=x,则ED=CD=AB=x,
∵AE=2,所以AD=AE+ED=2+x,
∴CG=CB=2+x,
∵AD∥BC,
∴∠AEG=∠CBH=∠CGH=∠AGE,
∴AG=AE=2,
∴AC=AG+CG=4+x,
在Rt△ABC中:AB2+BC2=AC2,
∴x2+(x+2)2=(x+4)2,解得x1=6,x2=﹣2(舍),
∴AB=CD=6,AD=AC=8,AC=BD=10,
∵AC与BD交于点O,
∴AO=BO=CO=DO=5,
∵sin∠BDA=![]() =
=![]() =
=![]() ,cos∠BDA=
,cos∠BDA=![]() =
=![]() =
=![]() ,
,
∴EF=![]() ED=
ED=![]() ,DF=
,DF=![]() ED=
ED=![]()
∴OF=OD﹣DF=5﹣![]() =
=![]()
在Rt△EFO中:
OE2=OF2+EF2=(![]() )2+(
)2+(![]() )2=
)2=![]() =13,
=13,
∴OE=![]() .
.
故答案为:![]()

练习册系列答案
相关题目