题目内容
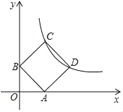
【题目】如图,正方形ABCD顶点C、D在反比例函数y=![]() (x>0)图象上,顶点A、B分别在x轴、y轴的正半轴上,则点C的坐标为_____.
(x>0)图象上,顶点A、B分别在x轴、y轴的正半轴上,则点C的坐标为_____.
【答案】(![]() ,2
,2![]() )
)
【解析】
要求C点的坐标,可设C点的坐标为(a,![]() ),作CE⊥y轴于E,FD⊥x轴于F,因为四边形ABCD是正方形,容易得出△BEC、△AOB、△DFA全等,从而可以用a表示出D点的坐标,从而构建方程解出a的值,则可求出C点的坐标.
),作CE⊥y轴于E,FD⊥x轴于F,因为四边形ABCD是正方形,容易得出△BEC、△AOB、△DFA全等,从而可以用a表示出D点的坐标,从而构建方程解出a的值,则可求出C点的坐标.
解:如图,过点C作CE⊥y轴于E,过点D做DF⊥x轴于F,
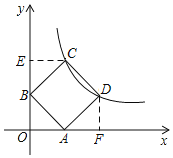
设C(a,![]() ),则CE=a,OE=
),则CE=a,OE=![]() ,
,
∵四边形ABCD为正方形,
∴BC=AB=AD,
∵∠BEC=∠AOB=∠AFD=90°,
∴∠EBC+∠OBA=90°,∠ECB+∠EBC=90°,
∴∠ECB=∠OBA,
同理可得:∠DAF=∠OBA,
∴Rt△BEC≌Rt△AOB≌Rt△DFA,
∴OB=EC=AF=a,
∴OA=BE=FD=![]() -a,
-a,
∴OF=a+![]() -a=
-a=![]() ,
,
∴点D的坐标为(![]() ,
,![]() -a),
-a),
把点D的坐标代入y=![]() (x>0),得到
(x>0),得到![]() (
(![]() -a)=6,解得a=-
-a)=6,解得a=-![]() (舍),或a=
(舍),或a=![]() ,
,
∴点C的坐标为(![]() ,2
,2![]() ),
),
故答案为:(![]() ,2
,2![]() ).
).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目