��Ŀ����
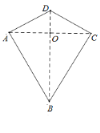
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����y��x��y����2x��ͼ��ֱ�Ϊֱ��l1��l2�����㣨��1��0����x��Ĵ��߽�l2�ڵ�A1������A1��y��Ĵ��߽�l1�ڵ�A2������A2��x��Ĵ��߽�l2�ڵ�A3������A3��y��Ĵ��߽�l1�ڵ�A4���������ν�����ȥ�����A2019�������ǣ�������
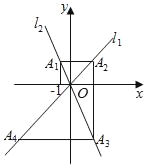
A. ����21008��21009��B. ��21008����21009��C. ��21009����21010�� D. ��21009��21010��
���𰸡�C
��������
�ֱ�д������An������꣬��������ı仯�ҳ��仯���ɣ�ÿ�ĸ������Ϊһ�����ڣ����˹��ɼ��ɵó����ۣ�
�⣺
��x����1ʱ��y��2��
���A1����������1��2����
��y��x��2ʱ��x��2��
���A2��������2��2��
ͬ���ɵã�A3��2����4����A4����4����4����A5����4��8����A6��8��8����
�۲�ɵõ�����Ϊ��
A1����������1��2����A5����22��23����
A2����������1��2����A6��23��23����
A3����������1��2����A7��23��-24����
A4����������1��2����A8����24��24����
��
�Դ����ƣ����Է�����4����Ϊһ���ڣ�
��2019��4��504��3�����Է���A2019��A3�ķ�����ͬ
n��1����һȦ����A3��21����22��
n��2���ڶ�Ȧ����A7��23����24��
��
n��505Ȧ��A2019��22n��1����22n����A2019��2505��2��1����22��505���ó�A2019��21009����21010��
��ѡ��C��

 �����ѧСѧ�꼶�νӽݾ��㽭��ѧ������ϵ�д�
�����ѧСѧ�꼶�νӽݾ��㽭��ѧ������ϵ�д�