题目内容
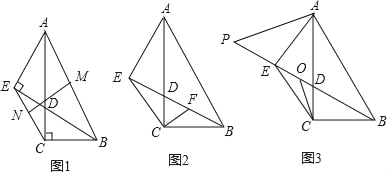
【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=2BC,点D在边AC上,连接BD,过A作BD的垂线交BD的延长线于点E.
(1)若M,N分别为线段AB,EC的中点,如图1,求证:MN⊥EC;
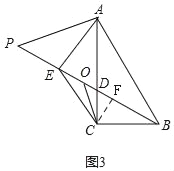
(2)如图2,过点C作CF⊥EC交BD于点F,求证:AE=2BF;
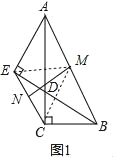
(3)如图3,以AE为一边作一个角等于∠BAC,这个角的另一边与BE的延长线交于P点,O为BP的中点,连接OC,求证:OC=![]() (BE﹣PE).
(BE﹣PE).
【答案】(1)详见解析;(2)详见解析;(3)详见解析.
【解析】
(1)连接EM、CM,直角三角形斜边上的中线等于斜边的一半得EM=CM;再由等腰三角形三线合一的性质得出结论;
(2)证明△AEC∽△BFC,得![]() 由AC=2BC得AE=2BF;
由AC=2BC得AE=2BF;
(3)证明△ACB∽△AEP,得![]() 从而知道AE=2PE,由AE=2BF得PE=BF;根据直角三角形斜边中线等于斜边一半得OC=
从而知道AE=2PE,由AE=2BF得PE=BF;根据直角三角形斜边中线等于斜边一半得OC=![]() EF,代入得结论.
EF,代入得结论.
证明:(1)如图1,连接EM、CM,
∵AE⊥BE,M是AB的中点,
∴EM=![]() AB,CM=
AB,CM=![]() AB,
AB,
∴EM=CM,
∵N是EC的中点,
∴MN⊥EC;
(2)如图2,∵∠ECF=90°,∠ACB=90°,
∴∠ECA+∠ACF=90°,∠ACF+∠FCB=90°,
∴∠ECA=∠FCB,
∵∠CFB=∠ECF+∠CEF=90°+∠CEF,
∠AEC=∠AEB+∠CEF=90°+∠CEF,
∴∠CFB=∠AEC,
∴△AEC∽△BFC,
∴![]()
∵AC=2BC,
∴AE=2BF;
(3)如图3,过点C作CF⊥EC交BD于点F,
∵∠AEP=∠ACB=90°,∠BAC=∠PAE,
∴△ACB∽△AEP,
∴![]()
∵AC=2BC,
∴AE=2PE,
∵AE=2BF,
∴PE=BF,
∵O为BP的中点,
∴PO=BO,
∴EO=FO,
∴CO=![]() EF=
EF=![]() (BE﹣BF)=
(BE﹣BF)=![]() (BE﹣PE).
(BE﹣PE).

【题目】已知二次函数y=ax2+bx+c(a≠0),函数y与自变量x的部分对应值如下表:
x | …… | ﹣1 | 0 | 1 | 4 | …… |
y | …… | 12 | 6 | 2 | 2 | …… |
(1)求二次函数的解析式;
(2)直接写出不等式ax2+bx+c﹣2>0的解集是 .