题目内容
【题目】在圆![]() 中,
中,![]() 、
、![]() 是圆
是圆![]() 的半径,点
的半径,点![]() 在劣弧
在劣弧![]() 上,
上,![]() ,
,![]() ,
,![]() ,连接
,连接![]() .
.

(1)如图1,试说明:![]() 平分
平分![]() ;
;
(2)如图2,点![]() 在弦
在弦![]() 的延长线上,连接
的延长线上,连接![]() ,如果
,如果![]() 是直角三角形,求
是直角三角形,求![]() 的长;
的长;
(3)如图3,点![]() 在弦
在弦![]() 上,与点
上,与点![]() 不重合,连接
不重合,连接![]() 与弦
与弦![]() 交于点
交于点![]() ,设点
,设点![]() 与点
与点![]() 的距离为
的距离为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() 的长为4或8;(3)
的长为4或8;(3)![]() ,
, ![]() .
.
【解析】
(1)由AO=BO知∠OAB=∠B,根据OB∥AC知∠B=∠CAB,据此可得∠OAB=∠CAB,即可得证;
(2)①∠AMB=90°时,作OH⊥AC可得AH=HC=![]() AC=6,由勾股定理求得OH=BM=8,根据矩形OBMH知HM=OB=10,由CM=HM-HC可得答案;②∠ABM=90°时,由①可知AB=8
AC=6,由勾股定理求得OH=BM=8,根据矩形OBMH知HM=OB=10,由CM=HM-HC可得答案;②∠ABM=90°时,由①可知AB=8![]() 、cos∠CAB
、cos∠CAB![]() ,在Rt△ABM中根据cos∠CAB=
,在Rt△ABM中根据cos∠CAB=![]() 可得AM=20,继而得出答案;
可得AM=20,继而得出答案;
(3)作OG⊥AB,由(1)知sin∠OAG=sin∠CAB,从而sin∠CAB=![]() ,结合OA=10求得OG=2
,结合OA=10求得OG=2![]() ,根据AC∥OB知
,根据AC∥OB知 ![]() ,即
,即![]() ,据此求得BE=
,据此求得BE=![]() ,利用y=
,利用y=![]() ×BE×OG可得答案.
×BE×OG可得答案.
(1)证明:∵![]() 、
、![]() 是圆
是圆![]() 的半径,
的半径,
∴![]() ∴
∴![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() 平分
平分![]() ;
;
(2)解:由题意可知![]() 不是直角,
不是直角,
所以![]() 是直角三角形只有以下两种情况:
是直角三角形只有以下两种情况:
![]() 和
和![]() ,
,
①当![]() ,点
,点![]() 的位置如图,
的位置如图,

过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,
,
∵![]() 经过圆心∴
经过圆心∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
在![]() 中,
中,![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴四边形![]() 是矩形,∴
是矩形,∴![]() ,
,
∴![]() ;
;
②当![]() ,点
,点![]() 的位置如图,
的位置如图,
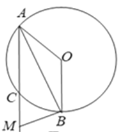
由①可得![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
![]() ,
,
综上所述,![]() 的长为4或8.
的长为4或8.
(3)过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,
,
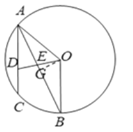
由(1)、(2)可知,![]() ,
,
由(2)可得:![]() ,
,
∵![]() ∴
∴![]() ,
,
∵![]() ∴
∴![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,
∴![]() ∴
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
自变量![]() 的取值范围为
的取值范围为![]() .
.

 名校课堂系列答案
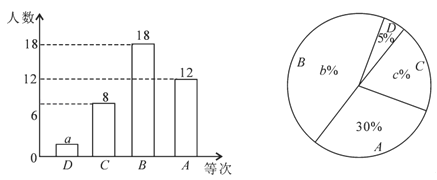
名校课堂系列答案【题目】某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
(1)则样本容量是 ,并补全直方图;
(2)该年级共有学生500人,请估计全年级在这天里发言次数不少于12的次数;
(3)已知A组发言的学生中恰有1位女生,E组发言的学生中有2位男生,现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率.
发言次数n | |
A | 0≤n<3 |
B | 3≤n<6 |
C | 6≤n<9 |
D | 9≤n<12 |
E | 12≤n<15 |
F | 15≤n<18 |