Question

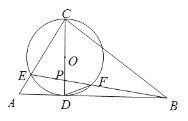
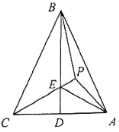
【题目】如图，P为等腰△ABC内一点，AB=BC，∠BPC=108°，D为AC中点，BD与PC相交于点E，已知P为△ABE的内心．

（1）求证：∠PEB=60°；

（2）求∠PAC的度数．

Answer 1

【答案】（1）见解析 （2）48°

【解析】

（1）先由P为△ABE的内心，∠BPC=108°易知∠BAE=36°，再由△ABC为等腰三角形，D为AC中点，∠BPC=108°得到∠CBE=∠ABE=2∠PBE，且∠CBP=∠BCP=∠BAE=36°，即可得到∠CBE=24°，再利用∠PEB=∠BCE+∠CBE得证.

（2）易知∠AED=∠CED=∠BEP=60°,从而得到∠EAD=30，利用∠PAC=∠EAD+∠PAE即可得解.

（1）∵P为△ABE内心，

∴PB、PE、PA分别是∠ABE、∠AEB、∠BAE角平分线；

即：∠PBE+∠PEB+∠PAE=90°，

又∵∠BPC=108°，

∴∠PBE+∠PEB=72°，

∴∠PAE=18°，∠BAE=36°；

∵AB=BC且D是AC中点，

∴∠ABE=∠CBE；BD⊥AC，

又∵BE=BE，AB=CB；

∴△ABE≌△CBE；即∠BCE=∠BAE=36°；

又∵∠BPC=108°，

∴∠CBP=36°，

∵又∠CBE=∠ABE=2∠PBE；

设∠PBE=∠ABP=x，则∠CBE=2x, 由∠CBP=∠CBE+∠PBE=36°,有2x+x=36°,

∴x=12°,

所以∠CBE=2x=24°，所以∠PEB=∠BCE+∠CBE=36°+2×14°=60°；

（2）由（1）知△ABE≌△CBE；

∴∠BEC=∠BEA，

∴∠CED=∠AED=∠PEB=60°；

∴∠EAD=30°，

∴∠PAC=∠EAD+∠PAE =30°+18°=48°。