题目内容
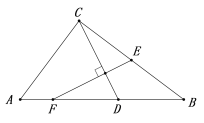
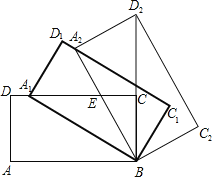
【题目】如图,矩形ABCD中,AB=m,BC=n,将此矩形绕点B顺时针方向旋转θ(0°<θ<90°)得到矩形A1BC1D1,点A1在边CD上.
(1)若m=2,n=1,求在旋转过程中,点D到点D1所经过路径的长度;
(2)将矩形A1BC1D1继续绕点B顺时针方向旋转得到矩形A2BC2D2,点D2在BC的延长线上,设边A2B与CD交于点E,若![]() =
=![]() ﹣1,求
﹣1,求![]() 的值.
的值.
【答案】(1)D到点D1所经过路径的长度为![]() π;(2)
π;(2)![]() (负根已经舍弃).
(负根已经舍弃).
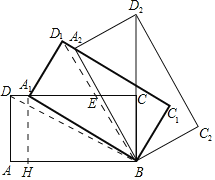
【解析】(1)作A1H⊥AB于H,连接BD,BD1,则四边形ADA1H是矩形.解直角三角形,求出∠ABA1,得到旋转角即可解决问题;
(2)由△BCE∽△BA2D2,推出![]() ,可得CE=
,可得CE=![]() ,由
,由![]() -1推出
-1推出![]() ,推出A1C=
,推出A1C=![]()
![]() ,推出BH=A1C=
,推出BH=A1C=![]()
![]() ,可得m2-n2=6
,可得m2-n2=6![]() ,可得1-
,可得1-![]() =6
=6![]() ,由此解方程即可解决问题;
,由此解方程即可解决问题;
(1)作A1H⊥AB于H,连接BD,BD1,则四边形ADA1H是矩形.
∴AD=HA1=n=1,
在Rt△A1HB中,∵BA1=BA=m=2,
∴BA1=2HA1,
∴∠ABA1=30°,
∴旋转角为30°,
∵BD=![]() ,
,
∴D到点D1所经过路径的长度=![]()
(2)∵△BCE∽△BA2D2,
∴![]() ,
,
∴CE=![]()
∵![]() -1
-1
∴![]() ,
,
∴A1C=![]()
![]() ,
,
∴BH=A1C=![]()
![]() ,
,
∴m2-n2=6![]() ,
,
∴m4-m2n2=6n4,
1-![]() =6
=6![]() ,
,
∴![]() (负根已经舍弃).
(负根已经舍弃).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
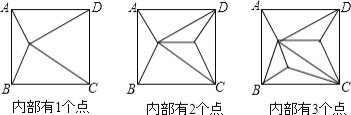
(1)填写下表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 4 | 6 |
|
| … |
|
(2)原正方形能否被分割成2019个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.