题目内容
【题目】在屋楼崮西侧一个坡度（或坡比）
的山坡
上发现有一棵古树
．测得古树底端
到山脚点
的距离
米，在距山脚点水平距离
米的点
处，测得古树顶端
的仰角
（古树与山坡的剖面、点在同一平面上，古树与直线
垂直），则古树的高度约为
（ ）
A.
米B.
米C.
米D.
米
【答案】A
【解析】
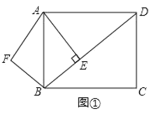
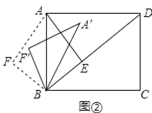
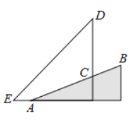
设CF=x，利用坡度写出AF长度，在直角三角形ACF中，利用勾股定理列出方程，解出x，进而得到EF长度，在直角三角形EDF中，利用三角函数解得DF，进而求出CD
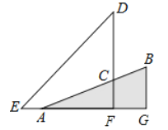
设CF为x,则AF为2x,有AC2=AF2+CF2,代入求得x=10,则AF=20．故EF=20+5=25
根据三角函数关系可得:
,解得DF=27.75．
∴DC=DF－CF=27.75－10=17.75．
故选A．
【题目】重庆一中各校区的中考体育学科考试在四月中旬圆满结束，在长期备战体考的过程中，学生的身体素质也在悄然发生变化．某体能测试机构将我校初三学生在体育测试中的成绩转换成弹跳力和臂力两项指标（百分制）作为体能测试成绩，并根据数据分析研究如何进一步提高学生的身体素质．
数据收集该机构计划选取100名学生的体能测试成绩作为样本，提供了以下三种抽样调查方法：
A．抽取初三年级皇冠校区的100名学生的体能测试成绩组成样本
B．抽取全年级体育成绩较好的学生共100名学生的体能测试成绩组成样本
C．从全年级中随机选取男、女各50名学生的体能测试成绩组成样本
数据整理与描述
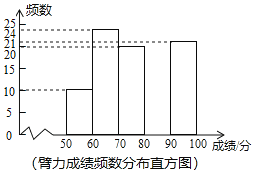
a．数据分成5组：90≤x≤100，80≤x＜90，70≤x＜80，60≤x＜70，50≤x＜60，其中90分以上为优秀．弹跳力成绩统计表和臂力成绩频数分布直方图如下：
弹跳力成绩 | 划记 | 人数 |
90≤x≤100 | p | |
80≤x＜90 | 正正正正正正丅 | 37 |
70≤x＜80 | 正正正正正 | 23 |
60≤x＜70 | 正一 | 6 |
50≤x＜60 | 正 | 5 |
合计 | 100 | 100 |
（弹跳力成绩统计表）
b．臂力成绩在70≤x＜80这一组的具体分数如下：
70 71 71 71.5 72 73 73.5 74 74 74
74.5 74.5 75 75.5 75.5 76 76 77 78 79
c．弹跳力和臂力两项指标成绩的平均数、中位数、众数、优秀率统计如下：
体能指标 | 平均数（分） | 中位数（分） | 众数（分） | 优秀率 |
弹跳力 | 82.5 | 89 | 83 | m |
臂力 | 77 | n | 81 | 21% |
数据分析根据以上信息，回答下列问题：
（1）上述三种抽样方法中，你认为最合理的是 （填字母）；
（2）补全臂力成绩频数分布直方图，并整理数据得，m＝ ，n＝ ；
（3）在此次测试中，某学生的弹跳力成绩为87分，臂力成绩为78分，这名学生成绩排名更靠前的指标是 （填“弹跳力”或“臂力”），理由是 ．
